
3. 若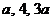 为等差数列的连续三项,则
为等差数列的连续三项,则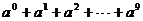 的值为( )
的值为( )
|
A. 1023 |
B.1025 |
C.1062 |
D. 2047 |
2. 若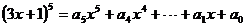 ,则
,则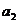 的值为( )
的值为( )
|
A.270 |
B.270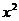 |
C. 90 |
D.90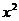 |
1. 集合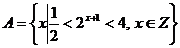 的元素个数有( )
的元素个数有( )
|
A. 1个 |
B. 2个 |
C.3个 |
D.无数个 |
20.(本小题共14分)
已知椭圆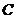 的焦点是
的焦点是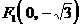 ,
,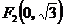 ,点
,点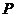 在椭圆上且满足
在椭圆上且满足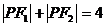 .
.
(Ⅰ)求椭圆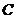 的标准方程;
的标准方程;
(Ⅱ)设直线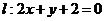 与椭圆
与椭圆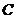 的交点为
的交点为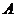 ,
,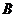 .
.
(i)求使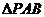 的面积为
的面积为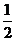 的点
的点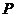 的个数;
的个数;
(ii)设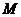 为椭圆上任一点,
为椭圆上任一点,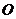 为坐标原点,
为坐标原点,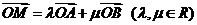 ,求
,求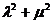 的值.
的值.
19. (本小题共14分)
设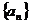 是正数组成的数列,其前
是正数组成的数列,其前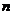 项和为
项和为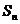 ,且对于所有的正整数
,且对于所有的正整数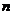 ,有
,有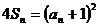 .
.
(I) 求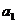 ,
,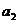 的值;
的值;
(II) 求数列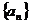 的通项公式;
的通项公式;
(III)令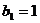 ,
,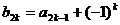 ,
,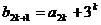 (
(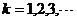 ),求
),求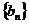 的前20项和
的前20项和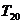 .
.
18. (本小题共13分)
已知函数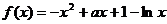 .
.
(Ⅰ)当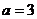 时,求函数
时,求函数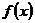 的单调递增区间;
的单调递增区间;
(Ⅱ)若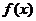 在区间
在区间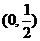 上是减函数,求实数
上是减函数,求实数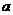 的取值范围.
的取值范围.
17. (本小题共13分)
口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5.甲先摸出一个球,记下编号为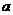 ,放回袋中后,乙再摸一个球,记下编号为
,放回袋中后,乙再摸一个球,记下编号为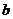 .
.
(Ⅰ)求“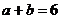 ”的事件发生的概率;
”的事件发生的概率;
(Ⅱ)若点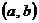 落在圆
落在圆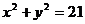 内,则甲赢,否则算乙赢,这个游戏规则公平吗?试说明理由.
内,则甲赢,否则算乙赢,这个游戏规则公平吗?试说明理由.
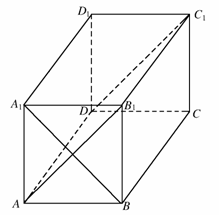
16. (本小题共13分)
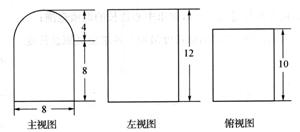
已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的数据,
(Ⅰ)求这个组合体的体积;
(Ⅱ)若组合体的底部几何体记为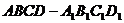 ,其中
,其中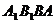 为正方形.
为正方形.
(i)求证: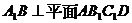 ;
;
 (ii)求证:
(ii)求证: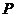 为棱
为棱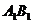 上一点,求
上一点,求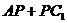 的最小值.
的最小值.
15.(本小题共13分)
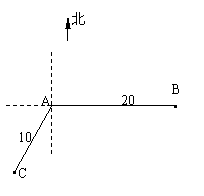 如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30
如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30 ,相距10海里C处的乙船.
,相距10海里C处的乙船.
(Ⅰ)求处于C处的乙船和遇险渔船间的距离;
(Ⅱ)设乙船沿直线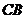 方向前往
方向前往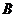 处救援,其方向与
处救援,其方向与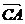 成
成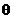 角,
角,
求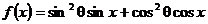 (x∈
(x∈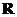 )的值域.
)的值域.
14.有下列命题:
①函数y=f (-x+2)与y=f (x-2)的图象关于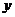 轴对称;
轴对称;
②若函数f(x)=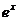 ,则
,则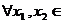
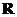 ,都有
,都有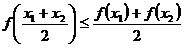 ;
;
③若函数f(x)=loga|
x |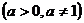 在(0,+∞)上单调递增,则f(-2)> f(a+1);
在(0,+∞)上单调递增,则f(-2)> f(a+1);
④若函数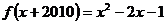 (x∈
(x∈ ),则函数f(x)的最小值为-2.
),则函数f(x)的最小值为-2.
其中真命题的序号是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com