
21.(本小题满分12分)
设A、B是椭圆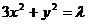 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点。
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点。
(1)确定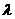 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(2)求以线段CD的中点M为圆心且与直线AB相切的圆的方程。
20.(本小题满分12分)
已知数列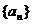 的前
的前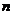 项和为
项和为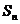 ,且
,且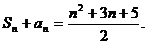
(1)证明:数列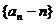 为等比数列;
为等比数列;
(2)设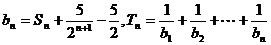 ,求证:
,求证: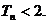
19.(本小题满分12分)
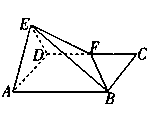
如图,平面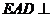 平面ABCD,
平面ABCD,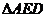 为正三角形,四边形ABCD为矩形,F是CD中点,EB与平面ABCD成30°角。
为正三角形,四边形ABCD为矩形,F是CD中点,EB与平面ABCD成30°角。
(1)当AD长度为何值时,点A到平面EFB的距离为2?
(2)二面角A-BF-E的大小是否与AD的长度有关?请说明。
18.(本小题满分12分)
某科技公司遇到一个技术难题,紧急成立了甲、乙两个攻关小组,这两个攻关小组按要求各自单独进行为期一个月的技术攻关,公司决定对攻关期满且攻克技术难题的小组给予奖励,已知此技术难题在攻关期满时被甲小组攻克的概率为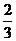 ,被乙小组攻克的概率为
,被乙小组攻克的概率为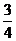 。
。
(1)设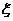 为攻关期满时获得奖励的攻关小组数,求
为攻关期满时获得奖励的攻关小组数,求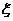 的分布列及E
的分布列及E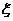 ;
;
(2)设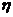 为攻关期满时获得奖励的攻关小组数与相应没有获得奖励的攻关小组数之差的平方,记“函数
为攻关期满时获得奖励的攻关小组数与相应没有获得奖励的攻关小组数之差的平方,记“函数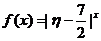 在定义域内单调递减”为事件C,求事件C的概率。
在定义域内单调递减”为事件C,求事件C的概率。
17.(本小题满分10分)
已知向量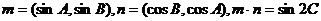 ,且A、B、C分别为
,且A、B、C分别为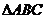 三边
三边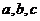 所对的角。
所对的角。
(1)求角C的大小;
(2)若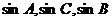 成等差数列,且
成等差数列,且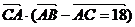 ,求
,求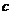 的长。
的长。
16.双曲线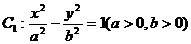 的左、右焦点分别为F1、F2,抛物线
的左、右焦点分别为F1、F2,抛物线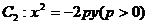 的焦点为F,C1与C2的一个交点为A,知A在
的焦点为F,C1与C2的一个交点为A,知A在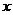 轴上的射影为F1,且A、F、F2三点共线,则双曲线C1的离心率为
。
轴上的射影为F1,且A、F、F2三点共线,则双曲线C1的离心率为
。
15.设随机变量X服从正态分布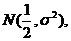 若
若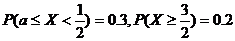 ,则
,则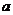 =
。
=
。
14.已知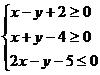 ,则
,则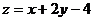 的最大值为
。
的最大值为
。
13.若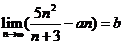 ,则实数
,则实数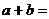 。
。
12.设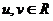 ,且
,且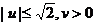 ,则
,则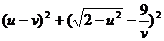 的最小值为 ( )
的最小值为 ( )
A.4 B.2 C.8 D.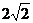
第Ⅱ卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com