
5.已知四边形ABCD,下列条件中,不能确定四边形ABCD是平行四边形的是( ▲ )
(A) AB∥CD且AD∥BC; (B) AB∥CD且 AB = CD ;
(C) AB∥CD且AD = BC;
(D) AB∥CD且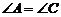 .
.
4.已知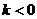 ,
,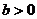 ,那么一次函数
,那么一次函数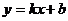 的大致图像是( ▲ )
的大致图像是( ▲ )
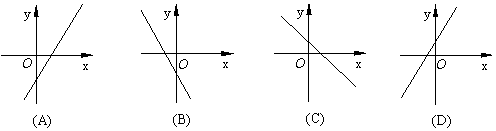
3.下列不等式组中,解集为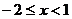 的是(
▲
)
的是(
▲
)
(A) 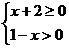 (B)
(B)
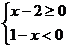 (C)
(C) 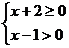 (D)
(D) 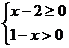
2.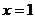 是下列哪个方程的解?( ▲ )
是下列哪个方程的解?( ▲ )
(A) 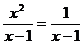 (B)
(B) 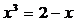 (C)
(C) 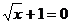 (D)
(D) 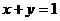
[每小题只有一个正确选项,在答题纸的相应题号的选项上用2 B铅笔填涂]
1.下列运算正确的是( ▲ )
(A) 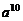 ÷
÷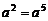 (B)
(B) 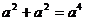 (C)
(C) 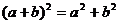 (D)
(D) 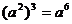
20.证明:
假设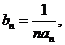 ∴
∴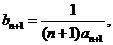 ………1分
………1分
∵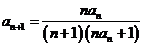 ,
,
∴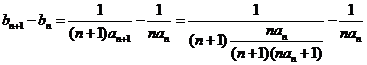 =
=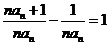
…………………………………3分
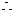
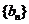 是首项为2,公差为1的等差数列.
………………………………4分
是首项为2,公差为1的等差数列.
………………………………4分
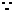
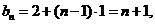
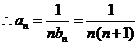 =
=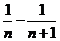 , …………6分
, …………6分
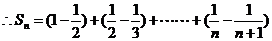 =
=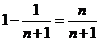 . …………8分
. …………8分
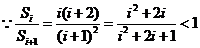 , …………………………………9分
, …………………………………9分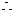
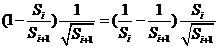
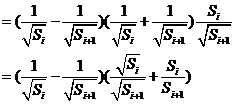
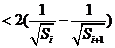 . …………………………………13分
. …………………………………13分
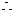
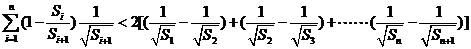
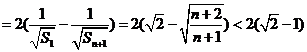 .…………16分
.…………16分



19.解: 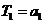 ,对
,对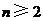 反复使用上述关系式,得
反复使用上述关系式,得
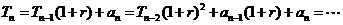
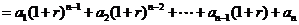 , ①
, ①
在①式两端同乘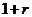 ,得
,得
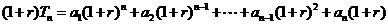 ②
②
②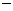 ①,得
①,得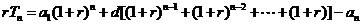
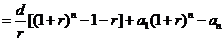 .
.
即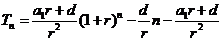 .
.
如果记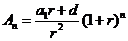 ,
,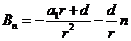 ,
,
则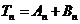 .
.
其中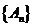 是以
是以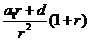 为首项,以
为首项,以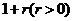 为公比的等比数列;
为公比的等比数列;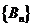 是以
是以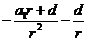 为首项,
为首项,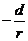 为公差的等差数列.
为公差的等差数列.
18.解:(I)证明:首先,由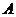 中元素构成的有序数对
中元素构成的有序数对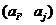 共有
共有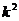 个.
个.
因为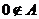 ,所以
,所以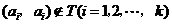 ;
;
又因为当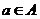 时,
时,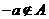 时,
时,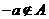 ,所以当
,所以当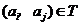 时,
时,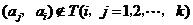 .
.
从而,集合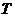 中元素的个数最多为
中元素的个数最多为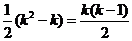 ,
,
即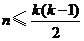 .
.
(II)解: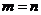 ,证明如下:
,证明如下:
(1)对于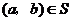 ,根据定义,
,根据定义,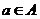 ,
,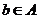 ,且
,且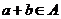 ,从而
,从而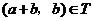 .
.
如果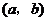 与
与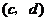 是
是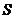 的不同元素,那么
的不同元素,那么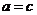 与
与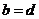 中至少有一个不成立,从而
中至少有一个不成立,从而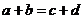 与
与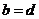 中也至少有一个不成立.
中也至少有一个不成立.
故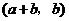 与
与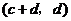 也是
也是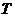 的不同元素.
的不同元素.
可见,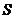 中元素的个数不多于
中元素的个数不多于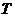 中元素的个数,即
中元素的个数,即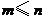 ,
,
(2)对于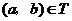 ,根据定义,
,根据定义,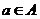 ,
,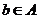 ,且
,且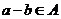 ,从而
,从而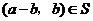 .如果
.如果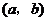 与
与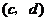 是
是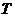 的不同元素,那么
的不同元素,那么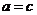 与
与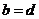 中至少有一个不成立,从而
中至少有一个不成立,从而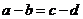 与
与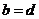 中也不至少有一个不成立,
中也不至少有一个不成立,
故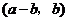 与
与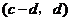 也是
也是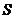 的不同元素.
的不同元素.
可见,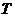 中元素的个数不多于
中元素的个数不多于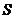 中元素的个数,即
中元素的个数,即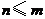 ,
,
由(1)(2)可知,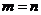 .
.
17. 解:(Ⅰ)∵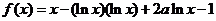 ,
,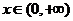
∴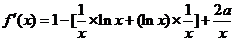 ,
,
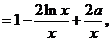 ……2分
……2分
∴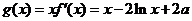 ,
,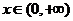
∴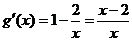 ,令
,令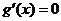 ,得
,得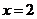 ,
……4分
,
……4分
列表如下:
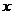 |
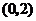 |
2 |
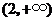 |
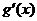 |
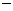 |
0 |
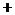 |
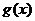 |
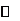 |
极小值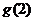 |
 |
∴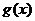 在
在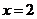 处取得极小值
处取得极小值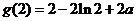 ,
,
即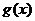 的最小值为
的最小值为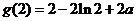 .
……6分
.
……6分
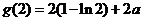 ,
,
∵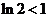 ,∴
,∴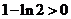 ,又
,又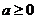 ,
,
∴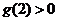 .
……8分
.
……8分
证明(Ⅱ)由(Ⅰ)知,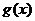 的最小值是正数,
的最小值是正数,
∴对一切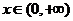 ,恒有
,恒有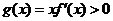 ,
……10分
,
……10分
从而当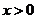 时,恒有
时,恒有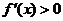 ,
……11分
,
……11分
故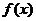 在
在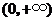 上是增函数.
……12分
上是增函数.
……12分
证明(Ⅲ)由(Ⅱ)知: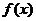 在
在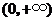 上是增函数,
上是增函数,
∴当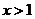 时,
时,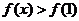 ,
……13分
,
……13分
又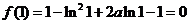 ,
……14分
,
……14分
∴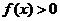 ,即
,即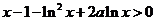 ,
……15分
,
……15分
∴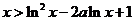
故当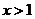 时,恒有
时,恒有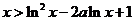 .
……16分
.
……16分
16. (1)∵PC⊥平面ABC,AB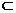 平面ABC,
平面ABC,
∴PC⊥AB。…………………… …2分
∵CD⊥平面PAB,AB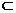 平面PAB,
平面PAB,
∴OC⊥AB。…………………… …4分
又PC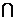 CD=C,
CD=C,
∴AB平面PCB。…………………… 4分
(2)过点A作AF//BC,且AF=BC,连接PF,CF。
则∠PAF为异面直线PA与BC所成的角。……………………5分
由(1)可得AB⊥BC,
∴CF⊥AF.
由三垂线定理,得PF⊥AF。
则AF=CF=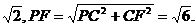
在Rt△PFA中,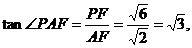
∴异面直线PA与BC所成的角为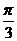 ……………………8分
……………………8分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com