
5.(2006陕西)设x,y为正数, 则(x+y)( + )的最小值为( )
A. 6 B.9 C.12 D.15
答案 B
解析 x,y为正数,(x+y)(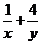 )≥
)≥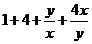 ≥9,选B.
≥9,选B.
4.(2006陕西)已知不等式(x+y)( + )≥9对任意正实数x,y恒成立,则正实数a的最小值为( )
A.2 B.4 C.6 D.8
答案 B
解析 不等式(x+y)(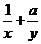 )≥9对任意正实数x,y恒成立,则
)≥9对任意正实数x,y恒成立,则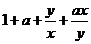 ≥
≥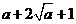 ≥9,∴
≥9,∴ 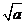 ≥2或
≥2或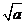 ≤-4(舍去),所以正实数a的最小值为4,选B.
≤-4(舍去),所以正实数a的最小值为4,选B.
3.(2006江苏)设a、b、c是互不相等的正数,则下列等式中不恒成立的是
A.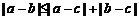 B.
B.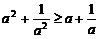
C.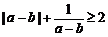 D.
D.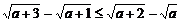
[思路点拨]本题主要考查.不等式恒成立的条件,由于给出的是不完全提干,必须结合选择支,才能得出正确的结论。
答案 C
解析 运用排除法,C选项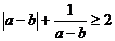 ,当a-b<0时不成立。
,当a-b<0时不成立。
[解后反思]运用公式一定要注意公式成立的条件
如果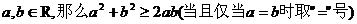
如果a,b是正数,那么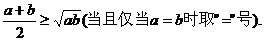
2.(2007北京)如果正数 满足
满足 ,那么( A )
,那么( A )
A.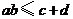 ,且等号成立时
,且等号成立时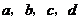 的取值唯一
的取值唯一
B.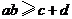 ,且等号成立时
,且等号成立时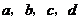 的取值唯一
的取值唯一
C.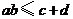 ,且等号成立时
,且等号成立时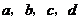 的取值不唯一
的取值不唯一
D.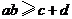 ,且等号成立时
,且等号成立时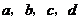 的取值不唯一
的取值不唯一
答案 A
1.(2008陕西)“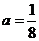 ”是“对任意的正数
”是“对任意的正数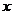 ,
,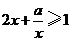 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
答案 A
4.(2009湖北卷文)(本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
解:(1)如图,设矩形的另一边长为a m
则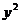 -45x-180(x-2)+180·2a=225x+360a-360
-45x-180(x-2)+180·2a=225x+360a-360
由已知xa=360,得a=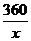 ,
,
所以y=225x+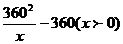


(II)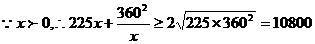

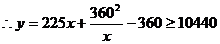 .当且仅当225x=
.当且仅当225x=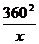 时,等号成立.
时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元. 

2005--2008年高考题
 3.(2009湖南卷文)若
3.(2009湖南卷文)若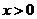 ,则
,则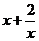 的最小值为
.
的最小值为
.
答案 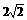 2
2
解析 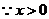
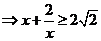 ,当且仅当
,当且仅当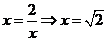 时取等号.
时取等号.
2.(2009重庆卷文)已知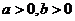 ,则
,则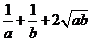 的最小值是( )
的最小值是( )
A.2 B.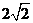 C.4 D.5
C.4 D.5
答案 C
解析 因为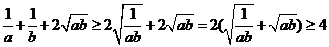 当且仅当
当且仅当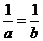 ,且
,即
,且
,即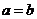 时,取“=”号。
时,取“=”号。
1.(2009天津卷理)设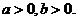 若
若 的最小值为
的最小值为
A . 8 B . 4 C.
1 D. 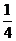
考点定位 本小题考查指数式和对数式的互化,以及均值不等式求最值的运用,考查了变通能力。
答案 C
解析 因为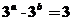 ,所以
,所以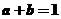 ,
,
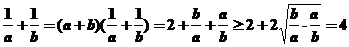 ,当且仅当
,当且仅当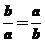 即
即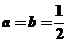 时“=”成立,故选择C
时“=”成立,故选择C
2009年高考题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com