
11. [答案]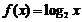 函数
函数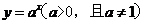 的反函数是
的反函数是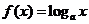 ,又
,又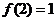 ,即
,即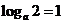 ,所以,
,所以,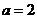 ,故
,故
10.[答案]:2 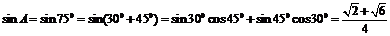
由a=c=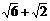 可知,
可知, ,所以
,所以 ,
, 由正弦定理得
由正弦定理得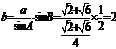 ,
,
1.[答案]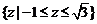 2.[答案]
2.[答案] 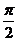 奇 3.[答案] 2 4、[答案]
奇 3.[答案] 2 4、[答案] 5、w[答案]1 6、[答案] 2 7.[答案]
5、w[答案]1 6、[答案] 2 7.[答案]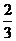 8. [答案]4条 9.[答案] 4
8. [答案]4条 9.[答案] 4
20.(本小题满分16分)
已知函数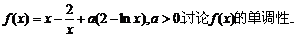
连云港市 高三数学信息试卷 第4页 (共4页)
连云港市2010届高考模拟卷
18.(本小题满分15分)
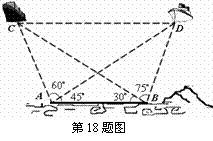
已知海岸边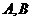 两海事监测站相距
两海事监测站相距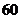
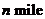 ,为了测量海平面上两艘油轮
,为了测量海平面上两艘油轮 间距离,在
间距离,在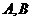 两处分别测得
两处分别测得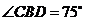 ,
,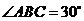 ,
, 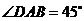 ,
,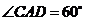
(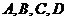 在同一个水平面内).请计算出
在同一个水平面内).请计算出 两艘轮船间距离.
两艘轮船间距离.
连云港市 高三数学信息试卷 第3页 (共4页)
19(本题满分16分)如图,抛物线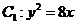 与双曲线
与双曲线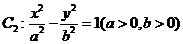 有公共焦点
有公共焦点 ,点
,点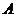 是曲线
是曲线 在第一象限的交点,且
在第一象限的交点,且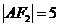 .
.
(Ⅰ)求双曲线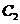 的方程;
的方程;
(Ⅱ)以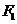 为圆心的圆
为圆心的圆 与双曲线的一条渐近线相切,圆
与双曲线的一条渐近线相切,圆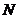 :
: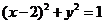 .平面上有点
.平面上有点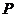 满足:存在过点
满足:存在过点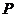 的无穷多对互相垂直的直线
的无穷多对互相垂直的直线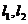 ,它们分别与圆
,它们分别与圆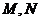 相交,且直线
相交,且直线 被圆
被圆 截得的弦长与直线
截得的弦长与直线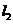 被圆
被圆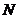 截得的弦长的比为
截得的弦长的比为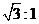 ,试求所有满足条件的点
,试求所有满足条件的点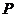 的坐标.
的坐标.
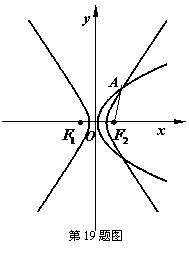
17.(本小题满分15分)
已知数列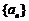 的通项公式为
的通项公式为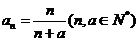
(1)若 成等比数列,求
成等比数列,求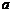 的值;
的值;
(2)当 且
且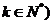 时,
时,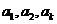 成等差数列,求
成等差数列,求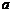 的值。
的值。
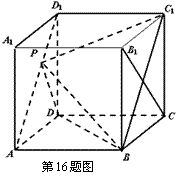
16.(本小题满分14分)
如图,在棱长为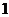 的正方体
的正方体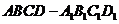 中,
中,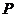 为线段
为线段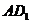 上的点,且满足
上的点,且满足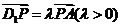 .
.
(Ⅰ)当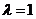 时,求证:平面
时,求证:平面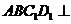 平面
平面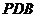 ;
;
(Ⅱ)试证无论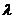 为何值,三棱锥
为何值,三棱锥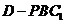 的体积恒为定值;
的体积恒为定值;
15.(本小题满分14分)已知函数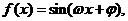 其中
其中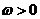 ,
,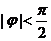
(I)若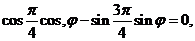 求
求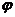 的值;
的值; 

(Ⅱ)在(I)的条件下,若函数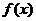 的图像的相邻两条对称轴之间的距离等于
的图像的相邻两条对称轴之间的距离等于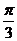 ,求函数
,求函数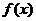 的解析式;并求最小正实数
的解析式;并求最小正实数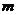 ,使得函数
,使得函数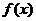 的图像象左平移
的图像象左平移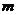 个单位所对应的函数是偶函数。
个单位所对应的函数是偶函数。
连云港市 高三数学信息试卷 第2页 (共4页)
20.(本小题满分16分)
已知函数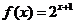 定义在R上.
定义在R上.
(Ⅰ)若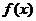 可以表示为一个偶函数
可以表示为一个偶函数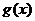 与一个奇函数
与一个奇函数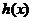 之和,设
之和,设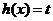 ,
,
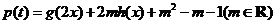 ,求出
,求出 的解析式;
的解析式;
(Ⅱ)若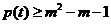 对于
对于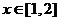 恒成立,求m的取值范围;
恒成立,求m的取值范围;
(Ⅲ)若方程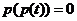 无实根,求m的取值范围.
无实根,求m的取值范围.
------------------------------------------------------------------------------------------------
江苏省扬州中学高三数学学科教研组制
高三 数学试卷 第4页 共4页
19.(本小题满分16分)
对于数列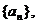
(1)已知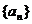 是一个公差不为零的等差数列,a5=6。
是一个公差不为零的等差数列,a5=6。
①当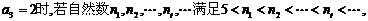
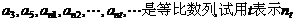 ;
;
②若存在自然数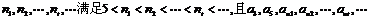 构成一个等比数列。求证:当a3是整数时,a3必为12的正约数。
构成一个等比数列。求证:当a3是整数时,a3必为12的正约数。
(2)若数列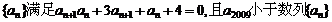 中的其他任何一项,求a1的取值范围
中的其他任何一项,求a1的取值范围
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com