
18.(本题满分12分)
为预防 病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
|
|
A组 |
B组 |
C组 |
|
疫苗有效 |
673 |
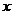 |
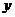 |
|
疫苗无效 |
77 |
90 |
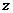 |
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(1)求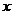 的值;
的值;
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取多少个?
(3)已知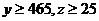 ,求不能通过测试的概率.
,求不能通过测试的概率.
 19. (本题满分12分)
19. (本题满分12分)
 在正三角形
在正三角形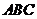 中,
中,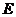 、
、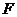 、
、 分别是
分别是 、
、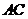 、
、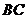 边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△
边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△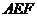 沿
沿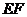 折起到
折起到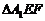 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小;
(Ⅲ)求二面角B-A1P-F的大小(用反三角函数表示)
17.(本题满分10分)
已知向量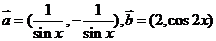 ,其中
,其中 .
.
(1)试判断向量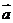 与
与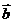 能否平行,并说明理由?
能否平行,并说明理由?
(2)求函数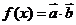 的最小值.
的最小值.
16.给出以下几个命题,正确的是 .
①函数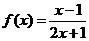 对称中心是
对称中心是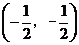 ;
;
②已知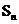 是等差数列
是等差数列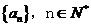 的前
的前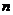 项和
,若
项和
,若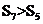 ,则
,则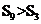 ;
;
③函数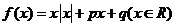 为奇函数的充要条件是
为奇函数的充要条件是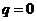 ;[
;[
④已知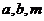 均是正数,且
均是正数,且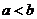 ,则
,则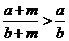 。
。
15. 下图(右)实线围成的部分是长方体(左)的平面展开图,其中四边形ABCD是边长为
下图(右)实线围成的部分是长方体(左)的平面展开图,其中四边形ABCD是边长为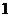 的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是
的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是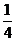 ,则此长方体的体积是 .
,则此长方体的体积是 .
14. 若点 为抛物线
为抛物线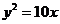 ,则点
,则点 到直线
到直线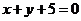 距离的最小值为
。
距离的最小值为
。
13.已知等差数列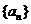 中,
中,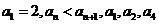 成等比数列,则
成等比数列,则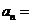 ______ _______.
______ _______.
12.已知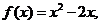 则满足条件
则满足条件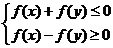 的点
的点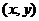 所形成区域的面积为( )
所形成区域的面积为( )
A.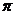 B.3 C.
B.3 C.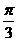 D.
D.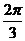
11.过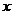 轴上一点
轴上一点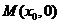 作圆
作圆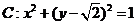 的两条切线,切点分别为
的两条切线,切点分别为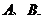
若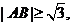 则
则 的取值范围是( )
的取值范围是( )
A.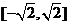 B.
B.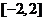 C.
C. D.
D.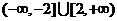
10. 将4个相同的白球和5个相同的黑球全部放入3个不同的盒子中,每个盒子既要有白球,又要有黑球,且每个盒子中球数不能少于2个,则所有不同的放法的种数为( )
A.12 B.3 C.18 D.6
9.已知棱长为3的正方体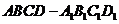 ,长为2的线段
,长为2的线段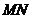 的一个端点
的一个端点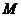 在
在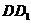 上运动,另一个端点
上运动,另一个端点 在底面
在底面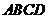 上运动.则线段
上运动.则线段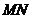 中点
中点 的轨迹与正方体的表面所围成的较小的几何体的体积为( )
的轨迹与正方体的表面所围成的较小的几何体的体积为( )
A.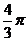 B.
B.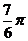 C.
C.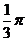 D.
D.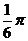
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com