
23. 如图,在某城市中,
如图,在某城市中,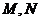 两地之间有整齐的方格形道路网,其中
两地之间有整齐的方格形道路网,其中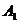 、
、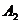 、
、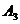 、
、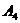 是道路网中位于一条对角线上的4个交汇处.今在道路网
是道路网中位于一条对角线上的4个交汇处.今在道路网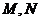 处的甲、乙两人分别要到
处的甲、乙两人分别要到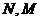 处,他们分别随机地选择一条沿街的最短路径,以相同的速度同时出发,直到到达
处,他们分别随机地选择一条沿街的最短路径,以相同的速度同时出发,直到到达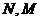 为止.
为止.
(1)求甲经过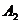 到达N的方法有多少种;
到达N的方法有多少种;
(2)求甲、乙两人在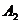 处相遇的概率;
处相遇的概率;
(3)求甲、乙两人相遇的概率.
解:(1)甲经过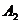 ,可分为两步:
,可分为两步:
第一步,甲从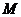 经过
经过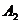 的方法数为
的方法数为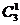 种;
种;
第二步,甲从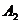 到
到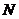 的方法数为
的方法数为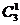 种;
种;
所以甲经过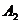 到达
到达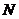 的方法数为
的方法数为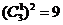 种.………………………………2分
种.………………………………2分
(2)由(1)知,甲经过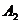 的方法数为
的方法数为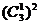 ;乙经过
;乙经过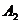 的方法数也为
的方法数也为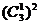 .
.
所以甲、乙两人在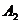 处相遇的方法数为
处相遇的方法数为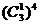 =81;
=81;
甲、乙两人在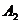 处相遇的概率为
处相遇的概率为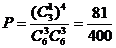 .………………………6分
.………………………6分
(3)甲、乙两人沿最短路径行走,只可能在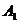 、
、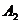 、
、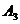 、
、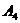 处相遇,他们在
处相遇,他们在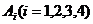 相遇的走法有
相遇的走法有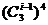 种方法;
种方法;
所以: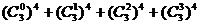 =164
=164
故甲、乙两人相遇的概率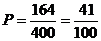 .
.
答:(1)甲经过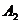 到达
到达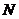 的方法数为
的方法数为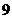 种;
种;
(2)甲、乙两人在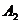 处相遇的概率为
处相遇的概率为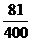 ;
;
(3)甲、乙两人相遇的概率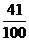 . ………………………10分
. ………………………10分
22.如图,在正方体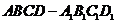 中,
中,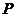 是棱
是棱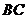 的中点,
的中点,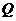 在棱
在棱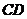 上.
上.

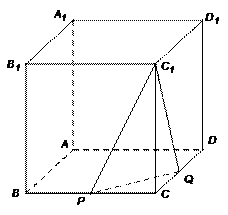 且
且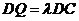 ,若二面角
,若二面角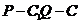 的余弦值为
的余弦值为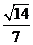 ,求实数
,求实数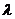 的值.
的值.
解:以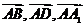 为正交基底,建立如图所示的空间直角坐标系
为正交基底,建立如图所示的空间直角坐标系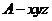 ,
,
设正方体的棱长为4,则各点的坐标分别为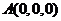 ,
,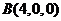 ,
,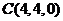 ,
,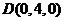 ;
;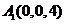 ,
,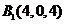 ,
,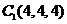 ,
,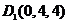 ,
,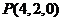 ,
,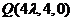 .………2分
.………2分
设平面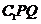 法向量为
法向量为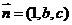 ,而
,而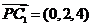 ,
,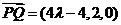 ,
,
所以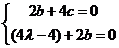 ,可得一个法向量
,可得一个法向量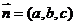 =
=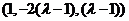 ,………6分
,………6分
设面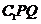 的一个法向量为
的一个法向量为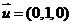 ,
,
则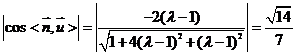 , …………………………8分
, …………………………8分
即: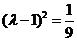 ,又因为点
,又因为点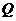 在棱
在棱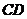 上,所以
上,所以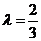 .……………………………10分
.……………………………10分
20.解:(1)因为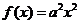 ,所以
,所以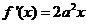 ,令
,令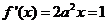
得: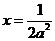 ,此时
,此时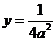 , …………2分
, …………2分
则点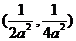 到直线
到直线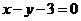 的距离为
的距离为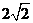 ,
,
即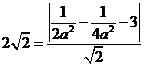 ,解之得
,解之得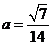 . …………4分
. …………4分
(2)解法一:不等式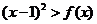 的解集中的整数恰有3个,
的解集中的整数恰有3个,
等价于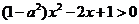 恰有三个整数解,故
恰有三个整数解,故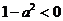 , …………6分
, …………6分
令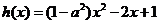 ,由
,由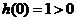 且
且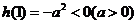 ,
,
所以函数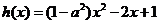 的一个零点在区间
的一个零点在区间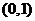 ,
,
则另一个零点一定在区间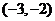 , …………8分
, …………8分
故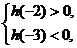 解之得
解之得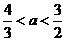 . …………10分
. …………10分
解法二: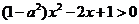 恰有三个整数解,故
恰有三个整数解,故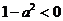 ,即
,即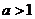 ,…………6分
,…………6分
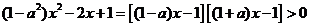 ,
,
所以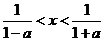 ,又因为
,又因为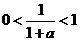 , …………8分
, …………8分
所以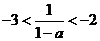 ,解之得
,解之得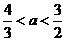 . …………10分
. …………10分
(3)设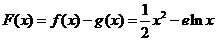 ,则
,则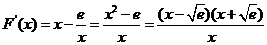 .
.
所以当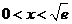 时,
时,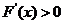 ;当
;当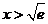 时,
时,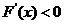 .
.
因此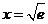 时,
时,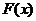 取得最小值
取得最小值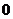 ,
,
则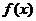 与
与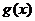 的图象在
的图象在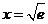 处有公共点
处有公共点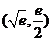 . …………12分
. …………12分
设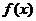 与
与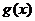 存在 “分界线”,方程为
存在 “分界线”,方程为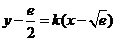 ,
,
即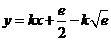 ,
,
由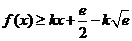 在
在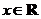 恒成立,则
恒成立,则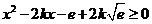 在
在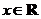 恒成立 .
恒成立 .
所以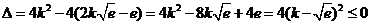 成立,
成立,
因此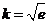 . …………14分
. …………14分
下面证明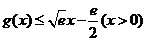 恒成立.
恒成立.
设 ,则
,则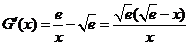 .
.
所以当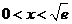 时,
时,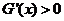 ;当
;当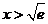 时,
时,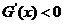 .
.
因此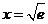 时
时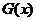 取得最大值
取得最大值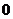 ,则
,则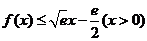 成立.
成立.
故所求“分界线”方程为: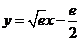 . …………16分
. …………16分
附加题部分
A.选修4-1(几何证明选讲)
如图,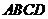 是边长为
是边长为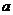 的正方形,以
的正方形,以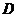 为圆心,
为圆心,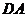 为半径的圆弧与以
为半径的圆弧与以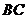 为直径的
为直径的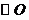 交于点
交于点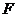 ,延长
,延长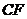 交
交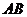 于
于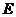 .(1)求证:
.(1)求证: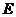 是
是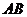 的中点;(2)求线段
的中点;(2)求线段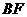 的长.
的长.
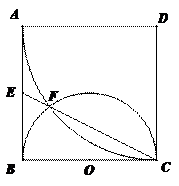
(1)证明:利用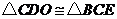 ,可证:
,可证: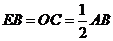
(2)由△FEB∽△BEC,得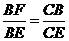 ,∴
,∴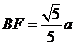 .
.
B.选修4-2(矩阵与变换)
已知矩阵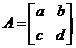 ,若矩阵
,若矩阵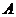 属于特征值3的一个特征向量为
属于特征值3的一个特征向量为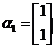 ,属于特征值-1的一个特征向量为
,属于特征值-1的一个特征向量为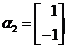 ,求矩阵
,求矩阵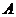 .
.
解:由矩阵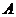 属于特征值3的一个特征向量为
属于特征值3的一个特征向量为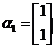 可得
可得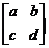
 =3
=3 ,
,
即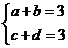 ;
…………………………………4分
;
…………………………………4分
由矩阵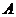 属于特征值2的一个特征向量为
属于特征值2的一个特征向量为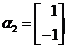 ,可得
,可得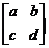
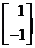 =(-1)
=(-1)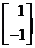 ,
,
即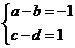 …………………………………………6分
…………………………………………6分
解得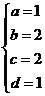 即矩阵
即矩阵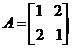 ………………10分
………………10分
C.选修4-4(坐标系与参数方程)
在极坐标系中,曲线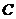 的极坐标方程为
的极坐标方程为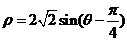 ,以极点为原点,极轴为
,以极点为原点,极轴为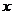 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线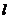 的参数方程为
的参数方程为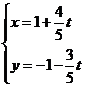 (
(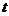 为参数),求直线
为参数),求直线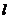 被曲线
被曲线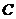 所截得的弦长.
所截得的弦长.
解:将方程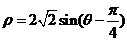 ,
,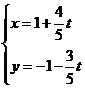 分别化为普通方程:
分别化为普通方程:
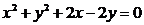 ,
, 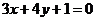 ………(6分)
………(6分)
由曲线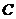 的圆心为
的圆心为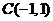 ,半径为
,半径为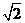 ,所以圆心
,所以圆心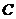 到直线
到直线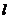 的距离为
的距离为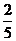 ,
,
故所求弦长为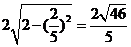 ………(10分)
………(10分)
D.选修4-5(不等式选讲)
已知实数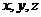 满足
满足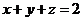 ,求
,求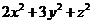 的最小值;
的最小值;
解:由柯西不等式可知: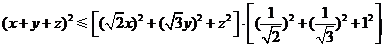
…………………………………………5分
故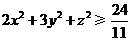 ,当且仅当
,当且仅当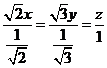 ,即:
,即: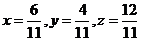
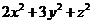 取得最小值为
取得最小值为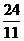 …………………………………………10分
…………………………………………10分
20.设函数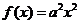 (
(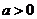 ),
),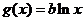 .
.
(1) 若函数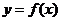 图象上的点到直线
图象上的点到直线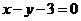 距离的最小值为
距离的最小值为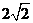 ,求
,求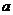 的值;
的值;
(2) 关于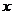 的不等式
的不等式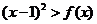 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数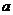 的取值范围;
的取值范围;
(3)
对于函数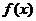 与
与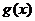 定义域上的任意实数
定义域上的任意实数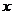 ,若存在常数
,若存在常数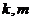 ,使得
,使得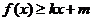 和
和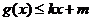 都成立,则称直线
都成立,则称直线 为函数
为函数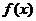 与
与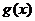 的“分界线”.设
的“分界线”.设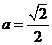 ,
,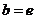 ,试探究
,试探究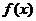 与
与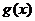 是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
19.(1)由题意得: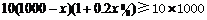 , …………………………4分
, …………………………4分
即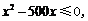 又
又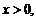 所以
所以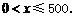
即最多调整500名员工从事第三产业.…………………………………………6分
(2)从事第三产业的员工创造的年总利润为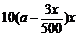 万元,从事原来产业的员工的年总利润为
万元,从事原来产业的员工的年总利润为
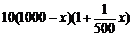 万元,则
万元,则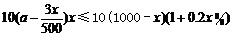 ,
,
…………………………………………10分
所以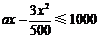
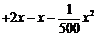 , 所以
, 所以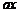
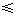
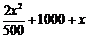 ,
,
即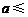
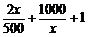 恒成立, …………………………………………12分
恒成立, …………………………………………12分
因为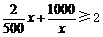
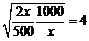 ,
,
当且仅当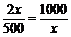 ,即
,即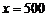 时等号成立.
时等号成立.
所以 , 又
, 又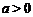 , 所以
, 所以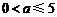 ,
,
即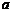 的取值范围为
的取值范围为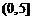 . …………………………………………16分
. …………………………………………16分
19.某单位有员工1000名,平均每人每年创造利润10万元。为了增加企业竞争力,决定优化产业结构,调整出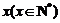 名员工从事第三产业,调整后他们平均每人每年创造利润为
名员工从事第三产业,调整后他们平均每人每年创造利润为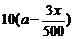 万元
万元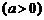 ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高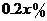 .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)在(1)的条件下,若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则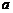 的取值范围是多少?
的取值范围是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com