
11.解析: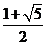 如图,∵
如图,∵ ,
,
∴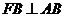 ,
,
 则
则 ,
,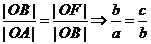

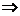
 ,∴
,∴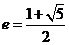
10. 解析: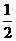 ∵
∵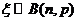 ,且
,且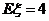 ,∴
,∴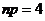 ,又∵
,又∵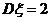 ,∴
,∴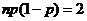 ,∴
,∴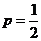
9. 解析: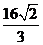 不等式
不等式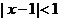 的解为
的解为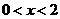 ,
,
由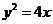 得
得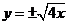
∴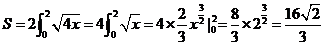 。
。
8. 解析:B.给5位同学按身高的不同由矮到高分别编
号为1,2,3,4,5,组成集合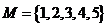
①若小组A中最高者为1,则能使B中最矮者高于A中最高者的小组B是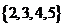 的非空子集,这样的子集有
的非空子集,这样的子集有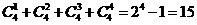 个,∴不同的选法有15个;②若A中最高者为2,则这样的小组A有2个:
个,∴不同的选法有15个;②若A中最高者为2,则这样的小组A有2个: 、
、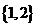 ,能使B中最矮者高于A中最高者的小组B是
,能使B中最矮者高于A中最高者的小组B是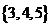 的非空子集,这样的子集(小组B)有
的非空子集,这样的子集(小组B)有 个,∴不同的选法有
个,∴不同的选法有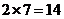 个;③若A中最高者为3,则这样的小组A有4个:
个;③若A中最高者为3,则这样的小组A有4个: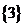 、
、 、
、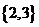 、
、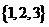 ,能使B中最矮者高于A中最高者的小组B是
,能使B中最矮者高于A中最高者的小组B是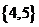 的非空子集,这样的子集(小组B)有
的非空子集,这样的子集(小组B)有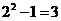 个,∴不同的选法有
个,∴不同的选法有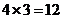 个;④若A中最高者为4,则这样的小组A有8个:
个;④若A中最高者为4,则这样的小组A有8个: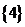 、
、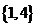 、
、 、
、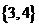 、
、 、
、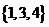 、
、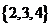 、
、 ,能使B中最矮者高于A中最高者的小组B只有
,能使B中最矮者高于A中最高者的小组B只有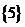 1个,∴不同的选法有8个。 ∴综上,所有不同的选法是
1个,∴不同的选法有8个。 ∴综上,所有不同的选法是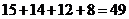 个,∴选B.
个,∴选B.
7.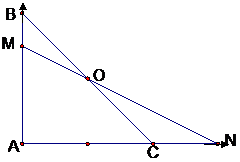 解析:B.以AC、AB为
解析:B.以AC、AB为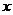 、
、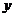 轴建立直角坐标系,设
轴建立直角坐标系,设
等腰直角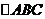 的腰长为2,则O点坐标为
的腰长为2,则O点坐标为
(1,1),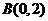 、
、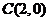 ,∵
,∵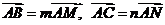 ,
,
∴ ,∴
,∴ 、
、 ,
,
∴直线MN的方程为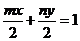 ,∵直线MN过点O(1,1),
,∵直线MN过点O(1,1),
∴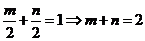
∵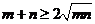 ,∴
,∴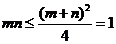 ,当且仅当
,当且仅当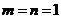 时取等号,∴
时取等号,∴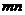 的最大值为1.
的最大值为1.
6.解析:B. 由复合命题真值表知:若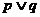 为真命题
为真命题
,则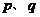 至少有一个为真命题,有可能一真一假,∴选项A错误;由
至少有一个为真命题,有可能一真一假,∴选项A错误;由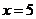 可以得到
可以得到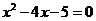 ,但由
,但由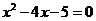 不一定能得到
不一定能得到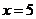 ,∴选项B成立;选项C错在把命题的否定写成了否命题;选项D错在没有搞清楚特称命题的否定是全称命题。
,∴选项B成立;选项C错在把命题的否定写成了否命题;选项D错在没有搞清楚特称命题的否定是全称命题。
5.解析:B 结合题意知该几何体是四棱锥,棱锥的的
底面是边长为8和6的长方形,棱锥的高是5,
∴由棱锥的体积公式得 ,故选B
,故选B
4.解析:C ∵等差数列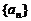 中
中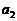 ,
,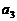 ,
,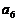 成等比数列,
成等比数列,
∴ ,即
,即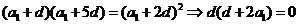
∵公差不为零,∴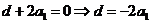 ,∴所求公比
,∴所求公比
3.解析:A 结合函数图像知:函数B、C、D 在区间(0,1)上都是减函数,只有A是增函数,故选A。
2.解析:D
由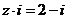 得,
得, ,∴选D
,∴选D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com