6. 若( 　)

A．　　　　　　　　　　　　　　 B．　　　　　　　　　　　 C．　　　　　　　　　　　 D．

5. 给出命题：(1)某彩票的中奖概率为，意味着买张彩票一定能中奖

(2)对立事件一定是互斥事件　

(3)若事件A、B满足P(A)+P(B)=1，则A、B为对立事件

(4)从装有2个红球和2个白球的口袋中任取2个球，记事件为“恰有1个白球”, 记事件为“恰有2个白球”，则为互斥而不对立的两个事件

其中正确命题的个数是　 ( 　)

A.3　　　　　 　B. 2　　　　　　 C. 1　　　　　　 D. 0

4. (＞0，＞0)在处取最大值，则 (　 )

A．一定是奇函数　　　 　　　 B．一定是偶函数

C．一定是奇函数　　　 　　　 D．一定是偶函数

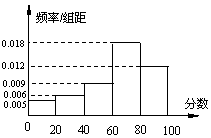
3. 如图是一次考试成绩的样本频率分布直方图(样本容量n=200)，若成绩不低于60分为及格，则样本中的及格人数是(　 )

A. 6　　 　　　　　B.36　　 　　　C. 60　 　　　　　D.120

2. 若向量和互相平行，其中，则(　　 )　 　

A. 或　　　 B. 　　　C. 或　　 　　D. 或

1. 下面命题中正确论述的命题个数是(　　 )

①求解某一类问题的算法是唯一的；

②任何一个算法都可能包含顺序结构、条件结构、循环结构；

③在“Scilab”程序语言中,赋值号与数学中的等号的意义相同。

④在“Scilab”程序语言中,赋值号左右能对换；

⑤循环结构中一定包含条件结构

A.1个　　　　　 B.2个　　　　 C.3个　　　　　　 D.4个

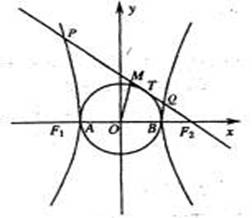
22．　 如图，已知双曲线(b>a>O)且[1，2]，它的左、右焦点分别为，左、右顶点分别为A、B．过作圆的切线，切点为T，交双曲线于P,Q两点.

(1)求证：直线PQ与双曲线的一条渐近线垂直；

(2)若M为的中点，0为坐标原点，∣OM∣-∣MT∣=1，∣PQ∣=∣AB∣，求实数的取值范围．

21．设，在处取得极大值，且存在斜率为的切线。

　 (1)求的取值范围；

　 (2)若函数在区间上单调递增，求的取值范围；

　 (3)是否存在的取值使得对于任意，都有。

20．某商店投入38万元经销某种纪念品，经销时间共60天，为了获得更多的利润，商店将每天获得的利润投入到次日的经营中，市场调研表明，该商店在经销这一产品期间第天的利润(单位：万元，)，记第n天的利润率，例如湖北

　 (1)求的值；湖北　 (2)求第天的利润率；湖北

　 (3)该商店在经销此纪念品期间，哪一天的利润率最大？并求该天的利润率。

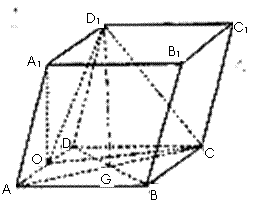
19、如图，平行六面体ABCD-中，底面ABCD是边长为2的菱形，∠BAD=，

　 　其中AC与BD交于点G，点在面ABCD上的射影0恰好为线段AD的中点。

(I)求点G到平面距离；

(Ⅱ)若与平面所成角的正弦值为，

　　　　 求二面角-OC-D的大小．