1．已知集合为　　　　　　 (　　 )

　　　 A．(1，2)　　　　　　　 B．　　　　　　　 C．　　　　　　　 D．

22．(11分)甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头，它们在一昼夜内任何时刻到达是等可能的．(1)如果甲船和乙船的停泊时间都是4小时，求它们中的任何一条船不需要等待码头空出的概率；(2)如果甲船的停泊时间为4小时，乙船的停泊时间是6小时，求它们中的任何一条船需要等待码头空出的概率．

.解略(1)　 25/36　　　　　 5分

　(2)　 107/288　　　　 6分

21、(11分) 某工厂对某产品的产量与成本的资料分析后有如下数据：

　　(Ⅰ) 画出散点图。

(Ⅱ) 求成本y与产量x之间的线性回归方程。(结果保留两位小数)

解：(I)图略　　 (4分)

　 (Ⅱ)解：设y与产量x的线性回归方程为

20．解：算法的功能为：_4分

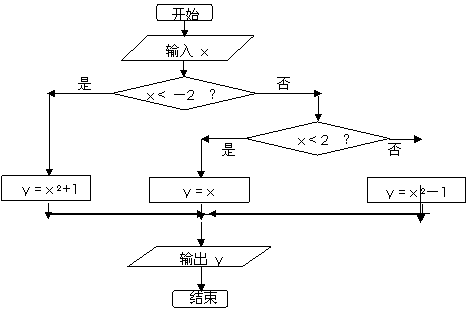　程序框图为：

　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　10分　　　　

18．(8分) 甲盒中有一个红色球，两个白色球，这3个球除颜色外完全相同，有放回地连续抽取2个，每次从中任意地取出1个球，用列表的方法列出所有可能结果，计算下列事件的概率。

(1)取出的2个球都是白球； (2)取出的2个球中至少有1个白球

.解略(1) 　(2)

解略(1)6/11　　 ( 4分 )　　　 (2)19　　 (4分)

17．(8分)对自行车运动员甲、乙两人在相同条件下进行了6次测试，测得他们的最大速度(m/s)的数据如下：

(3)　　 画出茎叶图，求中位数.

(4)　　 分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、方差，试判断选谁参加该项重大比赛更合适．

　　 思路解析：本题应用平均数和方差来解决实际问题．

　 解：(1)画茎叶图，中间数为数据的十位数　

从这个茎叶图上可以看出，乙的中位数是33.5，甲的中位数是33.　　　　　　 4分　　　

(2)：他们的平均速度为=(27+38+30+37+35+31)=33;

=(33+29+38+34+28+36)=33．

²=［(-6)²+5²+(-3)²+4²+2²+(-2)²］=；

²=［(-4)²+5²+1²+(-5)²+3²］=．　　　　　　　　　　　　　　　 8分

15．把下面求n！( n!= n×(n-1)×……×3×2×1 )的程序补充完整　 Input ， i<=n，　 s=s*i

________.　　　　

　x∈_[2kπ+π/6,2kπ+11π/6]　　 (k∈z)

13. 204与85的最大公约数是 ___17_______.

11.在长为10 cm的线段AB上任取一点P，并以线段AP为边作正方形，这个正方形的面积介于25 cm²与49 cm²之间的概率为(　 B )

A.　　　　　　　　 B.　　　　　　　　　 C.　　　　　　　　　 D.　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 B )　　　　　

A.-6/5　　　 B.- 5/6　　　　 C.3/4　　　 D.4/3

10.将一颗正方体型骰子投掷2次， 向上的点数之和是8的概率.　　　 (　　 C　 )

A.1/12　　　　　　　　 B.1/9　　　　　 C.5/36　 　　 D. 1/36