
23.解:(1)甲经过 到达N,可分为两步:第一步:甲从M经过
到达N,可分为两步:第一步:甲从M经过 的方法数:
的方法数: 种;第二步:甲从
种;第二步:甲从 到N的方法数:
到N的方法数: 种;所以:甲经过
种;所以:甲经过 的方法数为
的方法数为 ;
;
所以:甲经过 的概率
的概率
(2)由(1)知:甲经过 的方法数为:
的方法数为: ;乙经过
;乙经过 的方法数也为:
的方法数也为: ;所以甲、乙两人相遇经
;所以甲、乙两人相遇经 点的方法数为:
点的方法数为:  =81;
=81;
甲、乙两人相遇经 点的概率
点的概率
(3)甲、乙两人沿最短路径行走,只可能在 、
、 、
、 、
、 处相遇,他们在
处相遇,他们在 相遇的走法有
相遇的走法有 种方法;所以:
种方法;所以: =164甲、乙两人相遇的概率
=164甲、乙两人相遇的概率
22.(本小题满分10分)
解:(1)设过 作抛物线
作抛物线 的切线的斜率为
的切线的斜率为 ,则切线的方程为
,则切线的方程为 ,
,
与方程 联立,消去
联立,消去 ,得
,得 .
.
因为直线与抛物线相切,所以 ,
,
即 . 由题意知,此方程两根为
. 由题意知,此方程两根为 ,
,
∴ (定值). ………………………………5分
(定值). ………………………………5分
(2)设 ,由
,由 ,得
,得 .
.
所以在 点处的切线斜率为:
点处的切线斜率为: ,因此,切线方程为:
,因此,切线方程为: .
.
由 ,化简可得,
,化简可得, .
.
同理,得在点 处的切线方程为
处的切线方程为 .
.
因为两切线的交点为 ,故
,故 ,
, .
.
∴ 两点在直线
两点在直线 上,即直线
上,即直线 的方程为:
的方程为: .
.
当 时,
时, ,所以直线
,所以直线 经过定点
经过定点 . ………………………………10分
. ………………………………10分
21.B解:由题设得 ,设
,设 ,则
,则 . ………5分
. ………5分





 . ……10分
. ……10分
C解:(1)直线 普通方程为
普通方程为 ;
;
曲线 的普通方程为
的普通方程为 .
……………5分
.
……………5分
(2)∵ ,
, ,
,
∴点 到直线
到直线 的距离
的距离 点
点 到直线
到直线 的距离
的距离
∴ .
……………………………10分
.
……………………………10分
(D)(本小题满分10分)
证明:因为x,y,z都是为正数.所以 ,
,
同理可得 ,当且仅当x=y=z时,以上三式等号都成立.
,当且仅当x=y=z时,以上三式等号都成立.
将上述三个不等式两边分别相加,并除以2,得 . ………10分
. ………10分
21.A证:连结 ,因为
,因为 切圆
切圆 于
于 ,所以∠EAB=∠ACB。
,所以∠EAB=∠ACB。
因为弧 弧
弧 ,所以∠ACD=∠ACB,AB=AD,于是∠EAB=∠ACD………………5分
,所以∠ACD=∠ACB,AB=AD,于是∠EAB=∠ACD………………5分
又四边形ABCD内接于圆 ,所以∠ABE=∠D,所以△ABE∽CDA.
,所以∠ABE=∠D,所以△ABE∽CDA.
于是 ,即
,即 ,所以
,所以 ………………………10分
………………………10分
20. 解:(1)




 。
。
(2)原不等式代为 (1) 或
(1) 或  (2)
(2)
解(1)得: ;
;
解(2)得: 时,x<a;
时,x<a; 时,x<a且x≠a/2;
时,x<a且x≠a/2;
 时,x<a;
时,x<a; 时,
时, ;
;
 时,x<a.
时,x<a.


综合可知:
当 时,
时, ;
; 时,
时, ,且
,且 ;
;
 时,
时, .
.
说明:求解过程中,要比较a与 及a与
及a与 大小
大小
19.解:(1)由题意得
∴ . …………………………………3分
. …………………………………3分 
(2)当 时,
时,
∴ .----------5分
.----------5分
当 时,
时,


∴当第 个月的当月利润率
个月的当月利润率
 ……………………………9分
……………………………9分
(3)当 时,
时, 是减函数,此时
是减函数,此时 的最大值为
的最大值为 --11分
--11分
当 时,
时,
当且仅当 时,即
时,即 时,
时, ,又
,又 ,
,
∴当 时,
时, ……………………………………13分
……………………………………13分
答:该企业经销此产品期间,第40个月的当月利润率最大,最大值为 …14分
…14分
18.(1)解法一:过C作CH⊥x轴于H
设C(x0, )
)
∴MN=2MH= .
.
解法二:由题意得:⊙C的方程(x-x0)2+(y-y0)2=x02+(y0-1)2.
把y=0和x02=2py0代入整理得x2-2x0x+x02+xp2=0. 解之得方程的两根分为
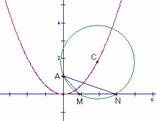 x1=x0-p,x2=x0+p. ∴ |MN|=|x1-x2|=2P.
x1=x0-p,x2=x0+p. ∴ |MN|=|x1-x2|=2P.
∴点C运动时,|MN|不会变化,|MN|=2P(定值)
(2)设∠MAN=
∵ |OA||MN|=p2,∴
|OA||MN|=p2,∴
∵ , ∴
, ∴ .
.
∴ .
.
∵只有当C在O点处时, 为直径上圆周角,其他时候都是劣弧上的圆周角.
为直径上圆周角,其他时候都是劣弧上的圆周角.
∴ ,
,
故当 时,原式有最大值
时,原式有最大值 .
.
∵∠MAN= ,∴∠MCN=2∠MAN=
,∴∠MCN=2∠MAN= ∴y0=P,x0=
∴y0=P,x0= ,r=
,r= .
.
所求圆的方程为
17.解(Ⅰ)由已知可得 ,则公差
,则公差 ,
,

(Ⅱ)最大的值是


 即
即 最大
最大
又当 时,
时, ;当
;当 时,
时, ,数列
,数列 递减
递减
所以, 最大
最大
16. 解:(Ⅰ)证明:取 的中点
的中点 ,连接
,连接 因为
因为 是正三角形,
是正三角形,
所以 又
又 是正三棱柱,所以
是正三棱柱,所以 面
面 ,所以
,所以
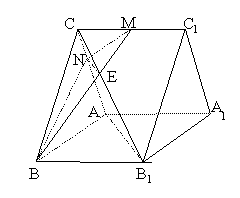 所以有
所以有 面
面 .因为
.因为 面
面
所以 ;
;
(Ⅱ) 为
为 的三等分点,
的三等分点, .
.
连结 ,
, ,
,
∵  ,∴
,∴  .
.
∴  , ∴
, ∴ 
又∵ 面
面 ,
, 面
面
 ∴
∴  平面
平面
15.(本小题满分12分)
(Ⅰ)解:由三角函数的定义,得点B的坐标
为 .
.
在 中,|OB|=2,
中,|OB|=2,
 ,
,
由正弦定理,得 ,即
,即 ,
,
所以  .
.
(Ⅱ)解:由(Ⅰ)得 ,---------7分
,---------7分
因为 ,
,
所以 ,
----------------------------9分
,
----------------------------9分
又

 , ---------------------------11分
, ---------------------------11分
所以 .
---------------------------12分
.
---------------------------12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com