
3、 的值为( )
的值为( )
(A)  (B)
(B) (C)
(C) (D)
(D) 
2、函数 的图像(( )
的图像(( )
(A) 关于原点对称
(B)关于主线 对称
对称
(C) 关于 轴对称
(D)关于直线
轴对称
(D)关于直线 对称
对称
1、设集合 ,则
,则 ( )
( )
(A) (B)
(B) (C)
(C) (D)
(D)
22.(本小题满分14分)
定义在 上的三个函数f(x)、g(x)、h(x),已知f(x)=
上的三个函数f(x)、g(x)、h(x),已知f(x)= ,
,
 ,且
,且 在
在 处取得极值.
处取得极值.
(1)求 的值及
的值及 的单调区间;
的单调区间;
(2)求证:当 ;
;
(3)把 对应的曲线
对应的曲线 向上平移6个单位后得到曲线
向上平移6个单位后得到曲线 ,求
,求 与
与 对应曲线
对应曲线 的交点的个数,并说明道理.
的交点的个数,并说明道理.

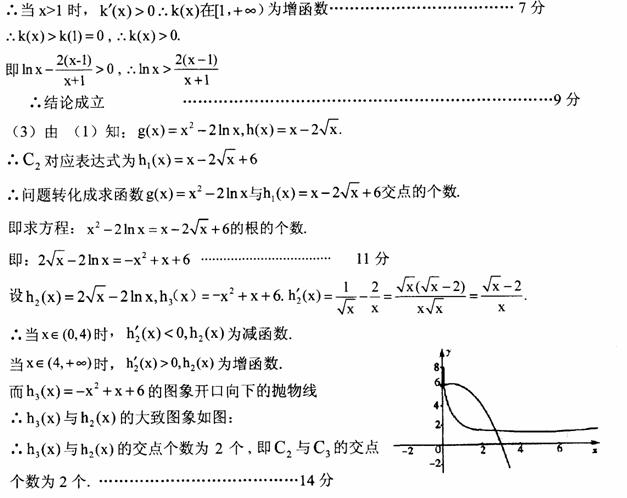
21.(I)解:因为椭圆一个顶点为(0, ),设椭圆的
),设椭圆的
方程为
直线 过原点,
过原点, 且<
且< ·
· >=
>= ,所以直线
,所以直线 的方程为
的方程为 ,或
,或
又| -
- | = |
| = |
 |.
|.
所以| | = |
| = | |.设|
|.设| |=m
|=m
又∠co F2= ,所以C点坐标(
,所以C点坐标( m,
m,  m)
m)
带入椭圆的方程为 得
得
 (
( m)2+
m)2+ (
( m)2=1 ①
m)2=1 ①
A2-2=m2 ②
解①②
故椭圆的方程为 ③
③
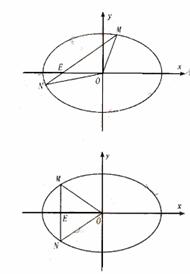
(II)解:设M( ),N(
),N( ).
).
当直线p不垂直 轴时,直线
轴时,直线 代入③,整理得
代入③,整理得



点O到直线MN的距离 ,
, cot∠MON≠0,
cot∠MON≠0,
 即
即 

即
整理得
当直线p垂直x轴时,也满足 .
.
故直线p的方程为
或 或
或
经检验上述直线均满足 .
.
所以所求直线p方程为 或
或 或
或
21.(本小题满分12分改编)
椭圆的中心在原点,焦点F1、F2在x轴,一个顶点为(0, ),过原点O的直线l和椭圆交于B,C.且<
),过原点O的直线l和椭圆交于B,C.且< ·
· >=
>= ,|
,| -
- |
= |
|
= | |.
|.
(Ⅰ)求椭圆C的方程;
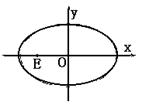
(Ⅱ)是否存在过点E(-2,0)的直线p交椭圆于点M、N,∠MON=θ(O为原点),使( ·
· )tanθ=
)tanθ= .若存在,求直线p的方程;
.若存在,求直线p的方程;
若不存在,请说明理由.
20. (本小题满分12分)
已知数列 的前
的前 项和为
项和为 且满足
且满足 ,
, 。
。
(I)
证明:{an- }为等比数列,并求数列
}为等比数列,并求数列 的通项公式;
的通项公式;
(II)
设
 为数列
为数列 的前
的前 项和,证明:
项和,证明: 。
。

19.解:(Ⅰ)∵点 分别是
分别是 、
、 的中点,
的中点,
∴  .
…… 2分
.
…… 2分
 ∴ ∠
∴ ∠ .
.
∴  又
又 ⊥
⊥ ,
,
∴  ∴
∴
∵  ,
,
∴  ⊥平面
⊥平面 .
…… 4分
.
…… 4分
∵  平面
平面 ,
,
∴  .
…… 6分
.
…… 6分
 (Ⅱ)建立如图所示的空间直角坐标系
(Ⅱ)建立如图所示的空间直角坐标系 .
.
则 (-1,0,0),
(-1,0,0), (-2,1,0),
(-2,1,0),
 (0,0,1).∴
(0,0,1).∴ =(-1,1,0),
=(-1,1,0),
 =(1,0,1), ……8分
=(1,0,1), ……8分
设平面 的法向量为
的法向量为 ,则
,则
 ……10分
……10分
令 ,得
,得 ,
,
∴  .
.
显然, 是平面
是平面 的一个法向量
的一个法向量 =(
=(
 ).
).
∴ cos< ,
, >=
>= .
.
∴ 二面角
 的余弦值是
的余弦值是 . ………………12分
. ………………12分
19. (本小题满分12分)
已知等腰直角三角形 ,其中∠
,其中∠ =90º,
=90º,  .点
.点 、
、 分别是
分别是 、
、 的中点,现将△
的中点,现将△ 沿着边
沿着边 折起到△
折起到△ 位置,使
位置,使 ⊥
⊥ ,连结
,连结 、
、 .
.
( Ⅰ)求证:
Ⅰ)求证: ⊥
⊥ ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
18.解:设指针落在A,B,C区域分别记为事件A,B,C.
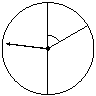 则
则 .
.  ………………3分
………………3分
(Ⅰ)若返券金额不低于30元,则指针落在A或B区域.
 ………………6分
………………6分
即消费128元的顾客,返券金 额不低于30元的概率是
额不低于30元的概率是 .
.
 (Ⅱ)由题意得,该顾客可转动转盘2次.
(Ⅱ)由题意得,该顾客可转动转盘2次.
随机变量 的可能值为0,30,60,90,120. ………………7分
的可能值为0,30,60,90,120. ………………7分

………………10分
所以,随机变量 的分布列为:
的分布列为:
 |
0 |
30 |
60 |
90 |
120 |
 |
 |
 |
 |
 |
 |
其数学期望 .………12分
.………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com