2.已知：点P的坐标(x，y)满足：及A(2，0)，则||·cos∠AOP(O为坐标原点)的最大值是　 5　 .

[解析]||·cos ∠AOP即为在上的投影长

由∴||·cos ∠AOP的最大值为5.

1.已知点的坐标满足条件 则的最大值为.

A. 　　　　 B. 8 　　　　C. 16　　　　　 　D.　 10

解析:画出不等式组对应的可行域如图所示：易得A(1，1)，OA＝,

B(2，2)，OB＝,C(1，3)，OC＝,故|OP|的最大值为，

即的最大值等于10.故选D.

6. 定义符合条件的有序数对为“和谐格点”，则当时，和谐格点的个

数是　　　　　　　　　 ．

[解析]作出可行域，数出和谐格点个数为7．

考点3 线性规划在实际问题中的应用

题型:在线性规划模型下的最优化问题.

.例1.(2008·揭阳一模) 为迎接2008年奥运会召开，某工艺品加工厂准备生产具有收藏价值的奥运会标志--“中国印·舞动的北京”和奥运会吉祥物--“福娃”.该厂所用的主要原料为A、B两种贵重金属，已知生产一套奥运会标志需用原料A和原料B的量分别为4盒和3盒，生产一套奥运会吉祥物需用原料A和原料B的量分别为5盒和10盒.若奥运会标志每套可获利700元，奥运会吉祥物每套可获利1200元，该厂月初一次性购进原料A、B的量分别为200盒和300盒.问该厂生产奥运会标志和奥运会吉祥物各多少套才能使该厂月利润最大，最大利润为多少？

[解题思路]将文字语言转化为数学式子建立线性规划模型.

解析:设该厂每月生产奥运会标志和奥运会吉祥物分别为套，月利润为元，由题意得

　()

目标函数为

作出可行域如图所示

目标函数可变形为，

∴当通过图中的点A时，最大，这时Z最大。

解得点A的坐标为(20,24)，　　　 …………10分

将点代入得元

答:该厂生产奥运会标志和奥运会吉祥物分别为20，24套时月利润最大，最大利润为42800元.

[名师指引]要注意到生产的产品数量是整数这一隐含条件.

★ 抢 分 频 道 ★

基础巩固训练

5. 已知满足约束条件,则的最小值是(　　 　)

A．　　　　　　　 B．　　　　　　　 C．　　　　　 　　 D．

解析:表示的可行域上的点与点的距离的平方值减1.选D

4. (广东省惠州市2009届高三第二次调研考试)设变量满足约束条件：，则的最小值(　　 )

A．　 　 B． 　 C．　 　　 D．

解析：画出可行域与目标函数线如下图可知，目标函数在点(－2，－2)取最小值－8．

∴选D．

3. 已知变量满足约束条件，则的取值范围是______.

解析：由得 ∴；

由得 ∴

∵表示过可行域内一点及原点的直线的斜率　

∴由约束条件画出可行域(如图)，则的取值范围为，即；

考点2　 线性规划中求目标函数的最值问题

题型: 求目标函数的最值

例1. 设，式中变量满足条件，求的最大值和最小值.

[解题思路]按解题步骤求解.

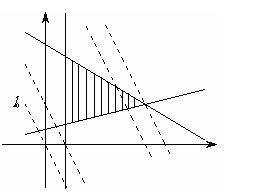[解析]作出可行域如图8-3-6所示,作直线:上,

　 作一组平行于的直线：，，

可知:直线往右平移时，随之增大。

由图象可知,当直线经过点时，对应的最大，

当直线经过点时，对应的最小，

　 所以，，．

[名师指引]要注意到线性目标函数的最大(小)值往往是在边界处取到.

例2. 已知满足不等式组，求使取最大值的整数．

[解题思路]先作平面区域,再作一组平行线：平行于：

_{进一步寻找整点.}

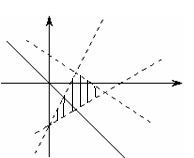[解析]不等式组的解集为三直线：，：，：所围成的三角形内部(不含边界)，设与，与，与交点分别为，则坐标分别为，，，

作一组平行线：平行于：，

当往右上方移动时，随之增大，

∴当过点时最大为，但不是整数解，

又由知可取，

当时，代入原不等式组得， ∴；

当时，得或， ∴或；

当时，， ∴，故的最大整数解为或．

[名师指引]在平行域内找整点最优解，一般采用平移找解法，即打网格，描整点，平移直线，找出最优解

[新题导练]

2.如果直线与圆相交于两点,且点关于直线对称,则不等式组所表示的平面区域的面积为________.

解析:因为M、N两点关于直线对称，所以直线的斜率，

而圆的圆心在直线上，所以，则不

等式组表示的平面区域就是一个斜边长为1的等腰直角三角形，面积为．

1. 图中阴影部分是下列不等式中(　 )表示的平面区域.

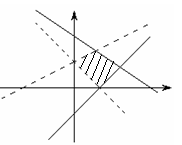A.　　　　 B.

　 C.　 　　　D.

解析:用原点作检验.选C