24．在中，AC=BC，，点D为AC的中点．

(1)如图1，E为线段DC上任意一点，将线段DE绕点D逆时针旋转90°得到线段DF，连结CF，过点F作，交直线AB于点H．判断FH与FC的数量关系并加以证明．

(2)如图2，若E为线段DC的延长线上任意一点，(1)中的其他条件不变，你在(1)中得出的结论是否发生改变，直接写出你的结论，不必证明．

23．已知：抛物线与轴有两个不同的交点．

(1)求的取值范围；

(2)当为整数，且关于的方程的解是负数时，求抛物线的解析式；

(3)在(2)的条件下，若在抛物线和轴所围成的封闭图形内画出一个最大的正方形，使得正方形的一边在轴上，其对边的两个端点在抛物线上，试求出这个最大正方形的边长．

22．已知正方形纸片ABCD的边长为2．

操作：如图1，将正方形纸片折叠，使顶点A落在边CD上的点P处(点P与C、D不重合)，折痕为EF，折叠后AB边落在PQ的位置，PQ与BC交于点G．

探究：(1)观察操作结果，找到一个与相似的三角形，并证明你的结论；

(2)当点P位于CD中点时，你找到的三角形与周长的比是多少(图2为备用图)？

21．如图，⊙O的直径AB=4，C、D为圆周上两点，且四边形OBCD是菱形，过点D的直线EF∥AC，交BA、BC的延长线于点E、F．

(1)求证：EF是⊙O的切线；

(2)求DE的长．

20．如图，在梯形ABCD中，AD//BC，BD⊥DC，

∠C=60°，AD=4，BC=6，求AB的长．

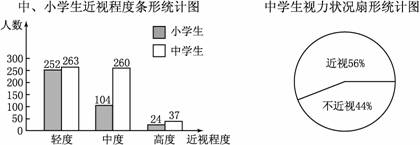
19．某市青少年健康研究中心随机抽取了本市1000名小学生和若干名中学生，对他们的视力状况进行了调查，并把调查结果绘制成如下统计图(近视程度分为轻度、中度、高度三种)．

(1)求这1000名小学生患近视的百分比；

(2)求本次抽查的中学生人数；

(3)该市有中学生8万人，小学生10万人.分别估计该市的中学生与小学生患“中度近视”的人数．

18．列方程或方程组解应用题：

在“五一”期间，小明、小亮等同学随家长一同到某公园游玩，下面是购买门票时，小明与他爸爸的对话(如图)，试根据图中的信息，解答下列问题：

(1)小明他们一共去了几个成人，几个学生？

(2)请你帮助小明算一算，用哪种方式购票更省钱？

17．已知正比例函数与反比例函数的图象交于两点，且点的坐标为．

(1)求正比例函数及反比例函数的解析式；

(2)在所给的平面直角坐标系中画出两个函数的图象，根据图象直接写出点的坐标及不等式的解集．

16．已知，求代数式的值．

15．已知：如图，AB=AC，点D是BC的中点，AB平分，

，垂足为E．

求证：AD=AE．