6．如图所示，一束细的复色光从空气中射到半球形玻璃体球心O点，经折射分为a、b两束光，分别由P、Q两点射出玻璃体。PP’、QQ’均与过O点的界面法线垂直。设光线a、b在玻璃体内穿行所用时间分别为t_a、t_b，则t_a: t_b等于

A. QQ’:PP’　　　 B.PP’:QQ’ 　　　C.OP’:OQ’　　 D.OQ’:OP’

5．关于相对论说法正确是

A．设某人在以速度为0.5c的飞船上，打开光源，飞船正前方地面上的观察者看到这一光速为1.5c

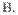高速运动的物体沿运动方向的长度变长

C．高速运动时物体质量总小于静止时的质量

D．在不同的惯性参考系中，一切物理定律都是相同的

4．摆长为L的单摆做简谐振动，若从某时刻开始计时，(取作t =0)，当振动至 　时，摆球具有负向最大速度，则单摆的振动图象是图中的

3．如图所示，位于介质I和II分界面上的波源S，产生两列分别沿x轴负方向与正方向传播的机械波。若在两种介质中波的频率及传播速度分别为f₁、f₂和v₁、v₂，则

A．f₁＝2f₂，v₁＝v₂ f₁＝f₂，v₁＝0.5v₂

C．f₁＝f₂，v₁＝2v₂　 　 D．f₁＝0.5f₂，v₁＝v₂

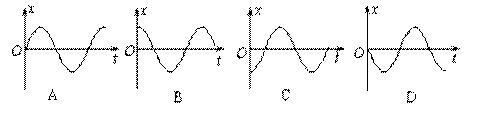
2．一列简谐横波在x轴上传播，某时刻的波形图如图所示，a 、b 、c为三个质点，a 正向上运动。由此可知

A．该波沿x 轴负方向传播　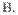 c 正向上运动

C．该时刻以后，b比c先到达平衡位置

D．该时刻以后，b比c先到达离平衡位置最远处

1．弹簧振子作简谐运动，t₁时刻速度为v，t₂时刻也为v，且方向相同。已知(t₂-t₁)小于周期T，则(t₂-t₁)

A．可能大于四分之一周期　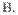　　　 一定小于四分之一周期

C．一定小于二分之一周期　　　　 D．可能等于二分之一周期

25．解：(1)由题意，得　 　解得　

∴直线的解析式为　 ．　 …………………………………　 1分

∵点在直线上，

∴．

∴．

∴直线的解析式为　 ．　 ………………………………　 2分

(2)① A点坐标为 (0，1)，

则点的纵坐标为1，设，

∴．

∴．

∴点的坐标为 ．　 …………………………………………　 3分

则点的横坐标为1，设

∴．

∴点的坐标为 ．　 …………………………………………　 4分

同理，可得　 ，．　 ………………………………　 6分

②经过归纳得　 ，．　 ………………　 7分

当动点到达处时，运动的总路径的长为点的横纵坐标之和再减去1，

即 ．　 ………………………………………　 8分

24．解：(1)FH与FC的数量关系是：． … 1分

证明：延长交于点G，

由题意，知　 ∠EDF=∠ACB=90°，DE=DF．

∴DG∥CB．

∵点D为AC的中点，

∴点G为AB的中点，且．

∴DG为的中位线．

∴．

∵AC=BC，

∴DC=DG．

∴DC- DE =DG- DF．

即EC =FG．　 ……………………………………………………………　 2分

∵∠EDF =90°，，

∴∠1+∠CFD =90°，∠2+∠CFD=90°．

∴∠1 =∠2．　 ……………………………………………………………　 3分

∵与都是等腰直角三角形，

∴∠DEF =∠DGA = 45°．

∴∠CEF =∠FGH = 135°．　 ……………………………………………　 4分

∴△CEF ≌△FGH．　 ………………………………………………………　 5分

∴ CF=FH．　 ………………………………………………………………　 6分

(2)FH与FC仍然相等．　 ………………………………………………　 7分

23．解：(1)，

依题意，得　

∴的取值范围是且．　 ①　 ……………………………　 2分

(2)解方程，得

．　 ……………………………………………………………　 3分

∵方程的解是负数，

∴．　 ∴．　　　 ②　 ………………………………　 4分

综合①②，及为整数，可得　 ．

∴抛物线解析式为　 ． 　………………………………　 5分

(3)如图，设最大正方形ABCD的边长为m，则B、C两点的纵坐标为，

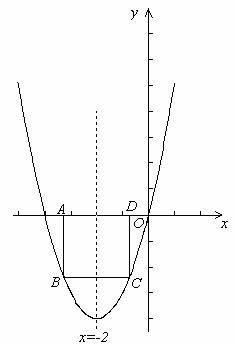且由对称性可知：B、C两点关于抛物线对称轴对称．

∵抛物线的对称轴为：．

∴点C的坐标为．　 ………………　 6分

∵C点在抛物线上，

∴．

整理，得　 ．

∴(舍负)

∴．　 ……………………　 7分

22．解：(1)与相似的三角形是．　 ………………………………　 1分

证明：∵四边形ABCD是正方形，

∴∠A=∠C=∠D=90°．

由折叠知　 ∠EPQ=∠A=90°．

∴∠1+∠3=90°，∠1+∠2=90°．

∴∠2=∠3．

∴∽．　 ………　 2分

(2)设ED=x，则AE=，

由折叠可知：EP=AE=．

∵点P是CD中点，

∴DP=1．

∵∠D=90°，

∴，

即

解得　 ．

∴．　 …………………………………………………………　 3分

∵∽，

∴．

∴与周长的比为4∶3．　 …………………………　 4分