21．(1)证明：∵AB是⊙O的直径，

∴∠ACB=90°．　 ……………………………………………………　 1分

∵四边形OBCD是菱形，

∴OD//BC．

∴∠1=∠ACB=90°．

∵EF∥AC，

∴∠2=∠1 =90°． ……………　 2分

∵OD是半径，

∴EF是⊙O的切线．　 …………………………………………　 3分

(2)解：连结OC，

∵直径AB=4，

∴半径OB=OC=2．

∵四边形OBCD是菱形，

∴OD=BC=OB=OC=2．　 …………………………………………　 4分

∴∠B=60°．

∵OD//BC，

∴∠EOD=∠B= 60°．

在Rt△EOD中，．…… 5分

20．解：过点A作AE⊥BD，垂足为E．

∵BD⊥DC，∠C=60°，BC=6，

∴∠1=30°，．　 ……………………　 1分

∵AD//BC，

∴∠2=∠1=30°．

∵AE⊥BD，AD=4，

∴，．　 ………　 3分

∴．　 …………………………………　 4分

∴．　 ……………………………………………　 5分

19．解：(1)，

∴这1000名小学生患近视的百分比为38%．　 ………………………　 2分

(2)抽查的中学生近视人数：263+260+37=560，

560÷56%=1000(人)，

∴本次抽查的中学生有1000人．　 ……………………………………　 4分

(3)∵8×=2.08(万人)，

∴该市中学生患“中度近视”的约有2.08万人．　 ……………………　 5分

∵10×=1.04(万人)，

∴该市小学生患“中度近视”的约有1.04万人．　 ……………………　 6分

18．解：(1)设去了x个成人，则去了(12- x)个学生，依题意，得

　　　　　 　………………………………………………　 2分

　　　　　 解得　 ．　 …………………………………………………………　 3分

　　　　　　　 ．

　　　　　 答：小明他们一共去了8个成人，4个学生．　 ………………………　 4分

　　　 (2)若按团体票购票：．

　　　　　　 ∵，　 ∴按团体票购票更省钱．　 ………………………　 5分

17．解：(1)∵点A 在正比例函数的图象上，

∴ ．

解得 ．

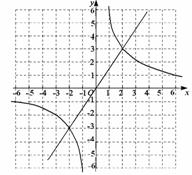∴ 正比例函数的解析式为 ． ………………………………　 1分

∵点A 在反比例函数的图象上，

∴ ．

解得 ．

∴ 反比例函数的解析式为．…… 2分

(2)点B的坐标为， …………… 3分

不等式的解集为或．　 …………………………　 5分

16．解：

　　　 　……………………………………………………　 2分

　　　 　　…………………………………………………………　 3分

　 　　　………………………………………………………………………　 4分

　　　 当，时，原式=．　 ………… 5分

15．证明：∵ AB=AC，点D是BC的中点，

∴ ∠ADB=90°．　 ………………… 1分

∵ AE⊥AB，

∴ ∠E=90°=∠ADB． ………………… 2分

∵ AB平分，

∴ ∠1=∠2．……………………………… 3分

在△ADB和△AEB中，

∴ △ADB≌△AEB．………………………………………………………　 4分

∴ AD=AE．………………………………………………………………… 5分

14．解：

　　　 ①+②，得　 ．

　　　　　　　　　 ．　 ……………………………………………………　 2分

　　　 把代入①，得

　　　　　　　　 ．

　　　　　　　　　 ．　 …………………………………………………　 4分

　　　 ∴原方程组的解为　 　……………………………………………　 5分

13．解：

　　　 　………………………………………………………　 4分

　　　 　　…………………………………………………………………　 5分

25．如图，直线：平行于直线，且与直线：相交于点．

(1)求直线、的解析式；

(2)直线与y轴交于点A．一动点从点A出发，先沿平行于x轴的方向运动，到达直线上的点处后，改为垂直于x轴的方向运动，到达直线上的点处后，再沿平行于x轴的方向运动，到达直线上的点处后，又改为垂直于x轴的方向运动，到达直线上的点处后，仍沿平行于x轴的方向运动，……

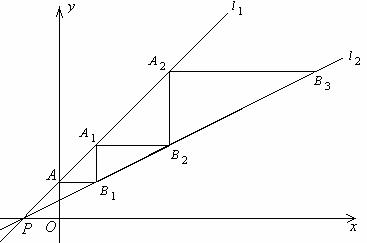照此规律运动，动点依次经过点，，，，，，…，，，…

①求点，，，的坐标；

②请你通过归纳得出点、的坐标；并求当动点到达处时，运动的总路径的长．

顺义区2010届初三第一次统一练习数学试卷答案及评分参考