1．的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．　　　　　 B．　　　　　 C．　　　　　　　　　 D．

21.(本小题满分14分)

已知函数，，数列满足：，

．

(1) 当时，求的值并写出数列的通项公式(不要求证明)；

(2) 求证：当时，；

(3) 求证：．

珠海市2009---2010学年度第二学期高考模拟测试

20.(本小题满分14分)

已知函数的图象过点，且在点处的切线与直线垂直．

(1) 求实数的值；

(2) 求在 (为自然对数的底数)上的最大值；

(3) 对任意给定的正实数，曲线上是否存在两点，使得是以为直角顶点的直角三角形，且此三角形斜边中点在轴上？

19.(本小题满分14分)

在中，点的坐标为(3，0)，且两端点、在轴上区间[-3，3]上滑动．

(1) 求的外心(三边垂直平分线的交点)的轨迹方程；

(2) 设直线与点的轨迹交于，两点，原点到直线的距离为，试求的值，使最大并求该最大值．

18.(本小题满分14分)

如图，在四棱锥中，为等边三角形，四边形为矩形，平面平面，分别是中点，．

(1) 求证：；

(2) 求二面角的余弦值．

17．(本小题满分12分)

如图是两个独立的转盘，在两个图中的四个扇形区域的圆心角分别为.用这两个转盘进行玩游戏，规则是：同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时，则这次转动无效，重新开始)，记转盘指针所对的区域数为，转盘指针所对的区域数为，，设的值为，每一次游戏得到奖励分为.

⑴求且的概率；

⑵某人进行了6次游戏，求他平均可以得到的奖励分．

16．(本小题满分12分)

如图，已知平面四边形中，为正三角形，

， ，记四边形的面积为.高☆考♂资♀源?网

(1) 将表示为的函数；　　

(2) 求的最大值及单调增区间．

15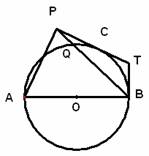．(几何证明选讲选做题)如图，为圆O的直径，为圆O上一点，和过的切线互相垂直，垂足为，过的切线交过的切线于，交圆O于，若，，则=　　　　 　.

14．(坐标系与参数方程选做题)已知曲线的极坐标方程是，以极点为平面直角坐标系的原点，极轴为轴的正半轴，建立平面直角坐标系，直线的参数方程是 (为参数)，则直线与曲线相交所成的弦的弦长为　　　．

13．方程的正整数解的个数为　　　　 ．