
21. 本题满分12分)
设f(x) 是定义在R上的减函数,满足f(x+y)=f(x)•f(y)且f(0)=1,数列{an}
满足a1=4,f(log3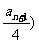 f(-1-log3
f(-1-log3 =1 (n∈N*);
=1 (n∈N*);
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Sn是数列{an}的前n项和, 试比较Sn与6n2-2的大小。
20. (本题满分12分)
(本题满分12分)
已知A﹑B﹑C是直线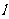 上的三点,向量
上的三点,向量 ﹑
﹑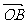 ﹑
﹑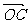 满足:
满足:
 -[y+2
-[y+2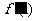 ]·
]·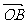 +ln(x+1)·
+ln(x+1)·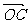 =
=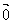 ;
;
(Ⅰ)求函数y=f(x)的表达式;
(Ⅱ)若x>0, 证明f(x)>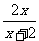 ;
;
(Ⅲ)当 时,x
时,x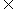
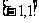 及b
及b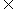
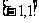 都恒成立,求实数m的取值范围。
都恒成立,求实数m的取值范围。
19. (本小题满分12分)
(本小题满分12分)
如图所示,三棱柱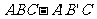 中,四边形
中,四边形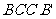 为菱形,
为菱形,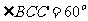 ,
,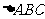 为等边三角形,面
为等边三角形,面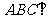 面
面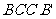 ,
,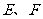 分别为棱
分别为棱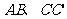 的中点;
的中点;
 (Ⅰ)求证:
(Ⅰ)求证: 面
面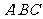 ';
';
 (Ⅱ)求二面角
(Ⅱ)求二面角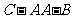 的大小。
的大小。
18.(本题满分12分)
已知某种植物种子每粒成功发芽的概率都为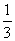 ,某植物研究所进行该种子的发芽实验,每次实验种一料种子,每次实验结果相互独立。假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的。若该研究所共进行四次实验,设
,某植物研究所进行该种子的发芽实验,每次实验种一料种子,每次实验结果相互独立。假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的。若该研究所共进行四次实验,设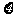 表示
四次实验结束时实验成功的次数与失败的次数之差的绝对值;
表示
四次实验结束时实验成功的次数与失败的次数之差的绝对值;
(Ⅰ)求随机变量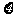 的数学期望E
的数学期望E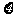 ;
;
 (Ⅱ)记“关于x的不等式
(Ⅱ)记“关于x的不等式  的解集是实数集R”为事件A,求事件A发生的概率P(A)。
的解集是实数集R”为事件A,求事件A发生的概率P(A)。
17.(本题满分10分)在△ABC中,a﹑b﹑c分别为三个内角A﹑B﹑C的对边,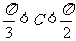 且
且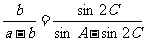 ;
;
(Ⅰ)判断△ABC的形状; (Ⅱ)若 ︱
︱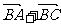 ︱=2,求
︱=2,求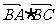 得取值范围。
得取值范围。
16.已知椭圆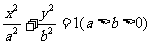 的右焦点为F(c,0),过F作与x轴垂直的直线与椭圆相交于点P,过点P的椭圆的切线
的右焦点为F(c,0),过F作与x轴垂直的直线与椭圆相交于点P,过点P的椭圆的切线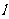 与x轴相交于点A,则点A的坐标为 ___。
与x轴相交于点A,则点A的坐标为 ___。
|
|
一年级 |
二年级 |
三年级 |
|
女生 |
373 |
 |
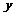 |
|
男生 |
377 |
370 |
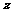 |
13.某校共有学生 名,各年级男、女生人数如下表.已知在全校学生中随机抽取
名,各年级男、女生人数如下表.已知在全校学生中随机抽取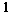 名抽到二年级女生的概率是
名抽到二年级女生的概率是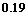 .现用分层抽样的方法在全校抽取
.现用分层抽样的方法在全校抽取 名学生,则应在三年级抽取的学生人数为_________。
名学生,则应在三年级抽取的学生人数为_________。
14若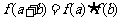 且f
(1)=2,则
且f
(1)=2,则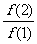 +
+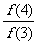 +
+ +…+
+…+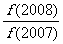 = ___ 。15.设地球半径为R,若甲地在北纬450,东经1200;乙地在北纬450,西经1500,则甲乙两地的球面距离为
。
= ___ 。15.设地球半径为R,若甲地在北纬450,东经1200;乙地在北纬450,西经1500,则甲乙两地的球面距离为
。
12.设函数f(x)=x3 ,若0≤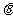 ≤
≤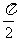 时,f(mcosθ)+f(1-m)>0恒成立,则实数m的取值范围是
( )
时,f(mcosθ)+f(1-m)>0恒成立,则实数m的取值范围是
( )
A.(0,1)
B.(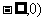 C. (
C. ( D. (
D. (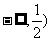
第Ⅱ卷
11.在平面直角坐标系中,不等式组 ,(a为常数)表示的平面区域的面积是9,那么a的值为
( )
,(a为常数)表示的平面区域的面积是9,那么a的值为
( )
A.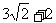 B.
B. 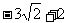 C.-5
D.1
C.-5
D.1
10.设a、b、c分别是ΔABC中∠A、∠B、∠C所对的边长,则直线xsinA+ay+c=0与bx-ysinB+sinC=0的位置关系是 ( )
A.平行 B.重合 C.垂直 D.相交但不垂直
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com