17．(本小题满分13分)

为保护水资源，宣传节约用水，某校4名志愿者准备去附近的甲、乙、丙三家公园进行宣传活动，每名志愿者都可以从三家公园中随机选择一家，且每人的选择相互独立.

(Ⅰ)求4人恰好选择了同一家公园的概率；

(Ⅱ)设选择甲公园的志愿者的人数为，试求的分布列及期望．

16．(本小题满分14分)

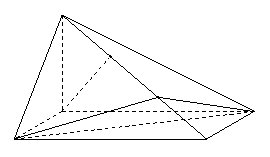已知四棱锥，底面为矩形，侧棱，其中，为侧棱上的两个三等分点，如图所示.

(Ⅰ)求证：；

(Ⅱ)求异面直线与所成角的余弦值；

(Ⅲ)求二面角的余弦值.

15．(本小题满分13分)

记等差数列的前n项和为，已知.

(Ⅰ)求数列的通项公式；

(Ⅱ)令，求数列的前n项和.

14．给定集合，映射满足：

①当时，；

②任取若，则有.

.则称映射：是一个“优映射”.例如：用表1表示的映射：是一个“优映射”.

　　　　　　　　　 表1　　　　　　　　　　　　　　　 表2

	1	2	3
	2	3	1

	1	2	3	4
		3

(1)已知表2表示的映射： 是一个优映射，请把表2补充完整(只需填出一个满足条件的映射)；

(2)若映射：是“优映射”，且方程的解恰有6个，则这样的“优映射”的个数是_____.

13．在中，角,,所对应的边分别为,,，若，则的最大值为　　　　　　 .

12.　 已知数列满足，(N)，则的值为　　　　　　 　.

11．已知向量a=，b=，若，则　　　　　 　；　　　 　.

10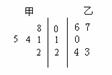．某校高中年级开设了丰富多彩的校本课程，甲、乙

两班各随机抽取了5名学生的学分，用茎叶图表示(如

右图).，分别表示甲、乙两班各自5名学生学分的

标准差，则　　 　　.(填“”、“”或“＝”)

9．在极坐标系中，若点()是曲线上的一点，则　　　 .

8．已知动圆C经过点(0，1),并且与直线相切，若直线与圆C有公共点，则圆C的面积

A．有最大值为　　　　　　　　　　　　　　　　　　　　　　　　　 B．有最小值为

C．有最大值为　　　 　　 　　　　　　　　　　　　　　　　　 D．有最小值为