
7. 已知温哥华冬奥会男子冰壶比赛8支球队中有3支弱队,以抽签的方式将这8支球队分成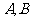 两组,每组4支,则
两组,每组4支,则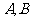 两组中有一组恰有两支弱队的概率为 ( )
两组中有一组恰有两支弱队的概率为 ( )
A.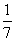 B.
B. 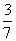 C.
C. 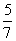 D.
D.
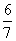
6. 对于下列结论,正确的是 ( )
①如果两条直线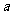 、
、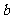 分别与直线
分别与直线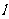 平行,那么
平行,那么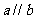
②如果两条直线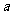 与平面
与平面 内的一条直线
内的一条直线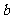 平行,那么
平行,那么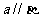
③如果直线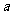 与平面
与平面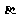 内的一条直线
内的一条直线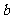 、
、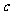 都有垂直,那么
都有垂直,那么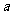 ⊥
⊥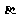
④如果平面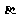 内的一条直线
内的一条直线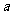 垂直平面
垂直平面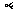 ,那么
,那么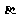 ⊥
⊥
A.①④ B. ①② C. ①③④ D.①②④
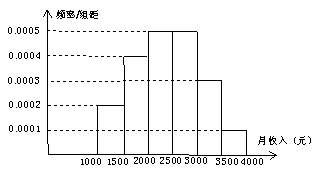
5. 一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图)。为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在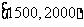 (元)月收入段应抽出的人数为
( )
(元)月收入段应抽出的人数为
( )
A.10 B.15 C.20 D.25
4. 已知数列{an}中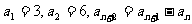 ,则
,则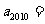 ( )
( )
 A.
A. 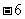 B.
B. 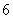 C.
C. 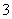 D.
D. 
3. 已知向量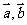 满足
满足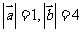 ,且
,且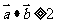 ,则
,则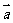 与
与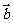 的夹角的取值范围是 ( )
的夹角的取值范围是 ( )
A.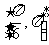 B.
B.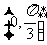 C.
C.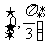 D.
D.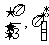
2.
函数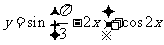 的最小正周期是
( )
的最小正周期是
( )
A.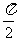 B.
B.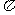 C.
C.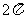 D.
D.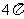
1.设全集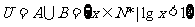 ,若
,若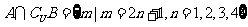 ,
,
则集合B= ( )
A{2,4,6,8} B{2,4,6,8,10} C{1,2,4,6,8} D{3,5,7,9}
22.(本小题满分14分)
设 的图象上任意两点,且
的图象上任意两点,且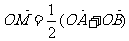 ,已知点M的横坐标为
,已知点M的横坐标为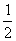 .
.
(I)求证:M点的纵坐标为定值;
(Ⅱ)若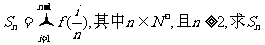 ;
;
(Ⅲ)已知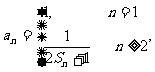 是否存在实数
是否存在实数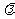 ,对于任意
,对于任意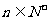 ,都有
,都有
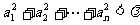 恒成立,若存在,求出
恒成立,若存在,求出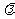 的值(或取值范围);若不存在,请说明理由.
的值(或取值范围);若不存在,请说明理由.
21.(本小题满分12分)
双曲线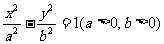 的离心率为2,坐标原点到直线AB的距离为
的离心率为2,坐标原点到直线AB的距离为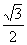 ,其中A(0,-b),B(a,0).
,其中A(0,-b),B(a,0).
(I)求双曲线的标准方程;
(Ⅱ)设F是双曲线的右焦点,直线l过点F且与双曲线的右支交于不同的两点P、Q,
且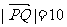 ,求直线l的方程.
,求直线l的方程.
20.(本小题满分12分)
正四棱柱ABCD-A1B1C1D1中,已知AB=2,E,F分别是D1B,AD的中点,
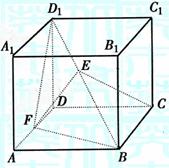
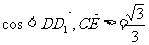 .
.
(I)建立适当的坐标系,求出E点的坐标;
(Ⅱ)证明:EF是异面直线D1B与AD的公垂线;
(Ⅲ)求二面角D1-BF-C的余弦值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com