
4.写出与下列各角终边相同的角的集合,并把集合中适合不等式-360o≤β<360o的元素写出来:
(1)60o (2)-75o (3) -824o30’ (4) 475o (5) 90o (6) 270o (7) 180o (8) 0o
C组:若
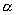 是第二象限角时,则
是第二象限角时,则 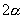 ,
, 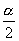 ,
,  分别是第几象限的角?
分别是第几象限的角?
3.写出终边在x轴上的角的集合。
2.在0o~360o范围内,找出下列各角终边相同的角,并指出它们是哪个象限的角:
(1)-265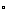 (2)-1000o (3)-843o10’ (4)3900o
(2)-1000o (3)-843o10’ (4)3900o
B组
A组:
1.与
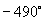 终边相同的角的集合是___________,它们是第____________象限的角,其中最小的正角是___________,最大负角是___________.
终边相同的角的集合是___________,它们是第____________象限的角,其中最小的正角是___________,最大负角是___________.
练习2 若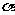 的终边在第一、三象限的角平分线上,则
的终边在第一、三象限的角平分线上,则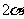 的终边在y轴的非负半轴上.
的终边在y轴的非负半轴上.
练习3 若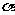 的终边与600角的终边相同,试写出在(00,3600)内,与
的终边与600角的终边相同,试写出在(00,3600)内,与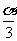 角的终边相同的角。 (200,1400,2600)
角的终边相同的角。 (200,1400,2600)
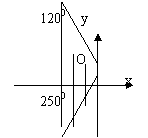
(备用题)练习4 如右图,写出阴影部分(包括边界)的角
的集合,并指出-950012,是否是该集合中的角。
({α| 1200+k×3600≤α≤2500+k×3600,k∈Z};是)
探究活动
经过5小时又25分钟,时钟的分针、时针各转多少度?
2. 要学会正确运用不等式进行角的表述同时要会以k取不同的值讨论型如
θ=a+k×1200(k∈Z)所表示的角所在的象限。
1. 要注意某一区间内的角和象限角的区别,象限角是由无数各区间角组成的;
例1写出与下列各角终边相同的角的集合S,并把S中适合不等式-3600≤β<7200的元素β写出来:
(1)600; (2)-210; (3)363014,
解:(1)S={β|β=600+k×3600,k∈Z}S中适合-3600≤β<7200的元素是
600+(-1)×3600=-3000 600+0×3600=600 600+1×3600=4200.
(2)S={β|β=-210+k×3600,k∈Z} S中适合-3600≤β<7200的元素是
-210+0×3600=-210 -210+1×3600=3390 -210+2×3600=6990
说明:-210不是00到3600的角,但仍可用上述方法来构成与-210角终边相同的角的集合。
(3)S={β|β=363014,+k×3600,k∈Z} S中适合-3600≤β<7200的元素是
363014,+(-2)×3600=-356046, 363014,+(-1)×3600=3014, 363014,+0×3600=363014,
说明:这种终边相同的角的表示法非常重要,应熟练掌握。
例2.写出终边在下列位置的角的集合
(1)x轴的负半轴上;(2)y轴上
分析:要求这些角的集合,根据终边相同的角的表示法,关键只要找出符合这个条件的一个角即α,然后在后面加上k×3600即可。
解:(1)∵在0○-360○间,终边在x轴负半轴上的角为1800,∴终边在x轴负半轴上的所有角构成的集合是{β|β=1800+k×3600,k∈Z }
(2)∵在0○-360○间,终边在y轴上的角有两个,即900和2700,∴与900角终边相同的角构成的集合是S1={β|β=900+k×3600,k∈Z }
同理,与2700角终边相同的角构成的集合是S2={β|β=2700+k×3600,k∈Z }
提问:同学们思考一下,能否将这两条式子写成统一表达式?
师:一下子可能看不出来,这时我们将这两条式子作一简单变化:
S1={β|β=900+k×3600,k∈Z }={β|β=900+2k×1800,k∈Z }………………(1)
S2={β|β=2700+k×3600,k∈Z }={β|β=900+1800+2k×1800,k∈Z }
={β|β=900+(2k+1)×1800,k∈Z } …………………(2)
师:在(1)式等号右边后一项是1800的所有偶数(2k)倍;在(2)式等号右边后一项是1800的所有奇数(2k+1)倍。因此,它们可以合并为1800的所有整数倍,(1)式和(2)式可统一写成900+n×1800(n∈Z),故终边在y轴上的角的集合为
S= S1∪S2 ={β|β=900+2k×1800,k∈Z }∪{β|β=900+(2k+1)×1800,k∈Z }
={β|β=900+n×1800,n∈Z }
处理:师生讨论,教师板演。
提问:终边落在x轴上的角的集合如何表示?终边落在坐标轴上的角的集合如何表示?
(思考后)答:{β|β=k×1800,k∈Z },{β|β=k×900,k∈Z }
进一步:终边落在第一、三象限角平分线上的角的集合如何表示?
答:{β|β=450+n×1800,n∈Z }
推广:{β|β=α+k×1800,k∈Z },β,α有何关系?(图形表示)
处理:“提问”由学生作答;“进一步”教师引导,学生作答;“推广”由学生归纳。
例1 若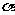 是第二象限角,则
是第二象限角,则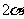 ,
,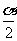 ,
,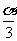 分别是第几象限的角?
分别是第几象限的角?
师: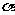 是第二象限角,如何表示?
是第二象限角,如何表示?
解:(1)∵ 是第二象限角,∴900+k×3600<
是第二象限角,∴900+k×3600< <1800+k×3600(k∈Z)
<1800+k×3600(k∈Z)
∴ 1800+k×7200<2 <3600+k×7200
<3600+k×7200
∴2 是第三或第四象限的角,或角的终边在y轴的非正半轴上。
是第三或第四象限的角,或角的终边在y轴的非正半轴上。
(2)∵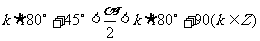 ,
,
处理:先将k取几个具体的数看一下(k=0,1,2,3…),再归纳出以下规律:
当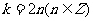 时,
时,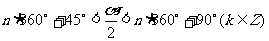 ,
,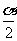 是第一象限的角;
是第一象限的角;
当 时,
时,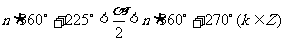 ,
,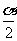 是第三象限的角。
是第三象限的角。
∴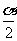 是第一或第三象限的角。
是第一或第三象限的角。
说明:配以图形加以说明。
(3)学生练习后教师讲解并配以图形说明。(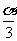 是第一或第二或第四象限的角)
是第一或第二或第四象限的角)
进一步求 是第几象限的角(
是第几象限的角( 是第三象限的角),学生练习,教师校对答案。
是第三象限的角),学生练习,教师校对答案。
师:上节课我们学习了角的概念的推广,推广后的角分为正角、负角和零角;另外还学习了象限角的概念,下面请一位同学叙述一下它们的定义。
生:略
师:上节课我们还学习了所有与α角终边相同的角的集合的表示法,[板书]
S={β|β=α+k×3600,k∈Z}
这节课我们将进一步学习并运用角的概念的推广,解决一些简单问题。
本节课我们学习了正角、负角和零角的概念,象限角的概念,要注意如果角的终边在坐标轴上,就认为这个角不属于任何象限,本节课的重点是学习终边相同的角的表示法。
判断一个角
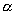 是第几象限角,只要把
是第几象限角,只要把 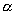 改写成
改写成 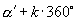 ,
, 
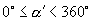 ,那么
,那么 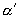 在第几象限,
在第几象限, 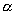 就是第几象限角,若角
就是第几象限角,若角 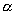 与角
与角  适合关系:
适合关系: 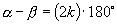 ,
, 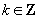 ,则
,则 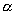 、
、  终边相同;若角
终边相同;若角 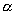 与
与  适合关系:
适合关系:  ,
, 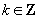 ,则
,则 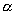 、
、  终边互为反向延长线.判断一个角所有象限或不同角之间的终边关系,可首先把它们化为:
终边互为反向延长线.判断一个角所有象限或不同角之间的终边关系,可首先把它们化为: 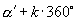 ,
, 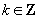 这种模式(
这种模式( 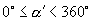 ),然后只要考查
),然后只要考查 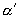 的相关问题即可.另外,数形结合思想、运动变化观点都是学习本课内容的重要思想方法.
的相关问题即可.另外,数形结合思想、运动变化观点都是学习本课内容的重要思想方法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com