设⊥平面AA₁D

∴平面AA₁C₁C的法向量

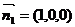
则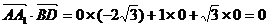

∴BD⊥AA₁……………………4分

  （Ⅱ）由于OB⊥平面AA₁C₁C

（Ⅰ）由于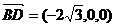

∴以OB．OC．OA₁所在直线为x轴．y轴．z轴建立如图所示空间直角坐标系，则A（0，－1，0），B（，0，0），C（0，1，0），D（－，0，0），A₁（0，0，）

……………………2分

15．解：

连接BD交AC于O，则BD⊥AC，

连接A₁O

在△AA₁O中，AA₁=2，AO=1，

∠A₁AO=60°

∴A₁O²=AA₁²+AO²－2AA₁?Aocos60°=3

∴AO²+A₁O²=A₁²

∴A₁O⊥AO，由于平面AA₁C₁C⊥

平面ABCD，

所以A₁O⊥底面ABCD

6,      7. （1，2）     8.      9.             10,    240         11,        12,             13．48     14．   ②④

1,                        2．        3．  ．       4．     5． ③

（2）设与圆相交与两点，求点到两点的距离之积.

09届高三数学天天练18答案