
(二)填空题
1.(北京卷文9)9.若角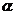 的终边经过点
的终边经过点 ,则
,则 的值为
.
的值为
.
[解析] [答案]
[答案]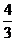
2.(浙江卷文12)若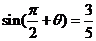 ,则
,则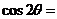 _________。
_________。
解析:本小题主要考查诱导公式及二倍角公式的应用。由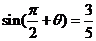 可知,
可知,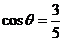 ;而
;而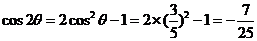 。答案:
。答案: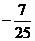
3.(上海春卷6)化简: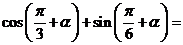 .
.

4.(广东卷理12)已知函数 ,
,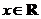 ,则
,则 的最小正周期是
.
的最小正周期是
.
[解析] ,此时可得函数的最小正周期
,此时可得函数的最小正周期 。
。
5.(江苏卷1)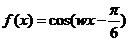 的最小正周期为
的最小正周期为 ,其中
,其中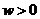 ,则
,则 。
。
[解析]本小题考查三角函数的周期公式.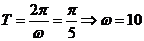 [答案]10
[答案]10
6.(辽宁卷理16)已知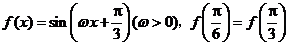 ,且
,且 在区间
在区间 有最小值,无最大值,则
有最小值,无最大值,则 =__________.
=__________.
解析:本小题主要针对考查三角函数图像对称性及周期性。依题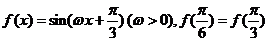 且
且 在区间
在区间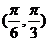 有最小值,无最大值,∴区间
有最小值,无最大值,∴区间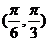 为
为 的一个半周期的子区间,且知
的一个半周期的子区间,且知 的图像关于
的图像关于 对称,∴
对称,∴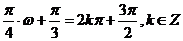 ,取
,取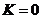 得
得 答案:
答案: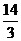
7.(辽宁卷文16)设 ,则函数
,则函数 的最小值为
.
的最小值为
.
解析:本小题主要考查三角函数的最值问题。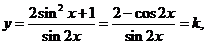
取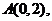
 的左半圆,作图(略)易知
的左半圆,作图(略)易知 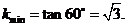 答案:
答案:
8.(上海卷理6)函数f(x)=sin x +sin(+x)的最大值是
[答案]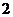
[解析]由 .
.
9.(上海春卷4)方程 在区间
在区间 内的解是
.
内的解是
.
解析:原方程就是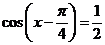 ,所以
,所以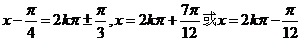
故在区间 内的解是
内的解是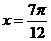 。
。
10.(四川延考理15)已知函数
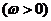 在
在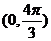 单调增加,在
单调增加,在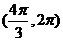 单调减少,则
单调减少,则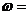 。
。
解:由题意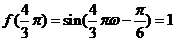

又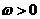 ,令
,令 得
得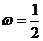 。(如
。(如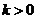 ,则
,则 ,
, 与已知矛盾)
与已知矛盾)
11.(四川延考文14)函数 的最大值是____________.
的最大值是____________.
解: 因为 ,
,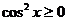 ,
, 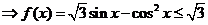 ,正好
,正好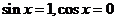 时取等号。(另
时取等号。(另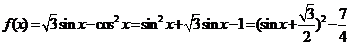 在
在 时取最大值)
时取最大值)
(一)选择题
1.(全国Ⅱ卷文1)若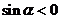 且
且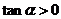 是,则
是,则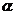 是( )
是( )
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
[解析]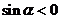 ,
,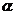 在三、四象限;
在三、四象限;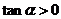 ,
,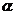 在一、三象限,∴选C
在一、三象限,∴选C
2.(陕西卷文1)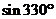 等于( )
等于( )
A.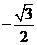 B.
B. C.
C. D.
D.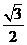
解:
3.(四川卷理5)若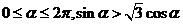 ,则
,则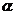 的取值范围是 ( )
的取值范围是 ( )
(A)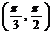 (B)
(B)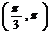 (C)
(C) (D)
(D)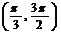
[解]:∵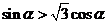 ∴
∴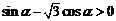 ,即
,即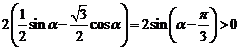
又∵ ∴
∴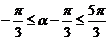 ,∴
,∴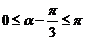 ,即
,即 故选C;
故选C;
[考点]:此题重点考察三角函数中两角和与差的正余弦公式逆用,以及正余弦函数的图象;
4.(四川延考文5)已知 ,则
,则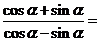 ( )
( )
A.2
B.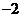 C.3
D.
C.3
D.
解:选C.
5.(海南宁夏卷理7)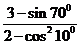 =( )
=( )
A.  B.
B.  C. 2 D.
C. 2 D. 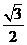
解: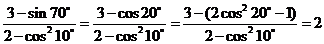 ,选C。
,选C。
6.(山东卷理5文10)已知cos(α-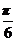 )+sinα=
)+sinα=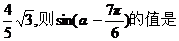
(A)-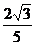 (B)
(B)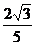 (C)-
(C)- (D)
(D) 
解: ,
,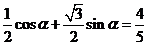 ,
,
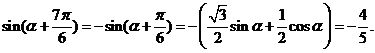
7.(四川卷理3文4)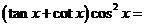 (
)
(
)
(A)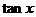 (B)
(B) (C)
(C)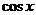 (D)
(D)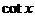
[解]:∵
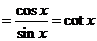 故选D;
故选D;
[点评]:此题重点考察各三角函数的关系;
8.(浙江卷理8)若 则
则 =( )
=( )
(A) (B)2
(C)
(B)2
(C)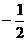 (D)
(D)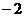
解析:本小题主要考查三角函数的求值问题。由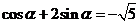 可知,
可知,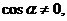 两边同时除以
两边同时除以 得
得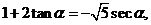 平方得
平方得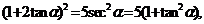
 ,解得
,解得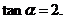 或用观察法.
或用观察法.
9.(四川延考理5)已知 ,则
,则 (
)
(
)
(A)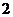 (B)
(B)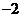 (C)
(C)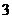 (D)
(D)
解: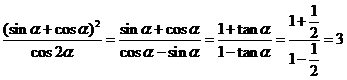 ,选C
,选C
10.(安徽卷文8)函数 图像的对称轴方程可能是( )
图像的对称轴方程可能是( )
A. B.
B.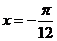 C.
C.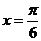 D.
D.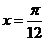
解: 的对称轴方程为
的对称轴方程为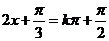 ,即
,即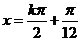 ,
,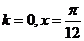
11.(广东卷文5)已知函数 ,则
,则 是( )
是( )
A、最小正周期为 的奇函数
B、最小正周期为
的奇函数
B、最小正周期为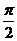 的奇函数
的奇函数
C、最小正周期为 的偶函数 D、最小正周期为
的偶函数 D、最小正周期为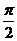 的偶函数
的偶函数
[解析]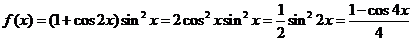 ,选D.
,选D.
12. (海南宁夏卷理1)已知函数y=2sin(ωx+φ)(ω>0)在区间[0,2π]的图像如下:那么ω=( )
(海南宁夏卷理1)已知函数y=2sin(ωx+φ)(ω>0)在区间[0,2π]的图像如下:那么ω=( )
A. 1 B. 2 C. 1/2 D. 1/3
解:由图象知函数的周期 ,所以
,所以
13.(海南宁夏卷文11)函数 的最小值和最大值分别为( )
的最小值和最大值分别为( )
A. -3,1 B.
-2,2 C.
-3,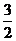 D.
-2,
D.
-2,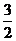
[标准答案]:C
[试题解析]:∵
∴当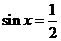 时,
时,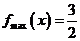 ,当
,当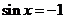 时,
时,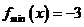 ;故选C;
;故选C;
[高考考点]三角函数值域及二次函数值域
[易错点]:忽视正弦函数的范围而出错。
[全品备考提示]:高考对三角函数的考查一直以中档题为主,只要认真运算即可。
14.(湖南卷理6)函数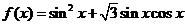 在区间
在区间 上的最大值是( )
上的最大值是( )
A.1
B. C.
C. 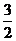 D.1+
D.1+
[答案]C
[解析]由 ,
,
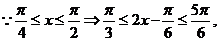
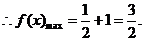 故选C.
故选C.
15.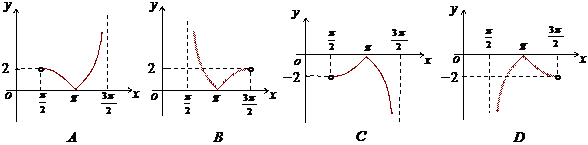 (江西卷理6文10)函数
(江西卷理6文10)函数 在区间
在区间 内的图象是
内的图象是
[解析]D. 函数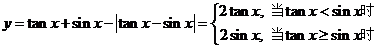
16.(江西卷文6)函数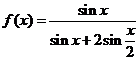 是
是
A.以 为周期的偶函数
B.以
为周期的偶函数
B.以 为周期的奇函数
为周期的奇函数
C.以 为周期的偶函数
D.以
为周期的偶函数
D.以 为周期的奇函数
为周期的奇函数
[解析]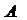
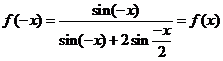
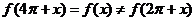
17.(全国Ⅰ卷理8)为得到函数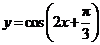 的图像,只需将函数
的图像,只需将函数 的图像( )
的图像( )
A.向左平移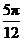 个长度单位 B.向右平移
个长度单位 B.向右平移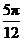 个长度单位
个长度单位
C.向左平移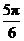 个长度单位 D.向右平移
个长度单位 D.向右平移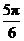 个长度单位
个长度单位
[解析].A. 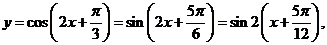 只需将函数
只需将函数 的图像向左平移
的图像向左平移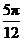 个单位得到函数
个单位得到函数 的图像.
的图像.
18.(全国Ⅰ卷文6) 是( )
是( )
A.最小正周期为 的偶函数 B.最小正周期为
的偶函数 B.最小正周期为 的奇函数
的奇函数
C.最小正周期为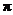 的偶函数 D.最小正周期为
的偶函数 D.最小正周期为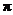 的奇函数
的奇函数
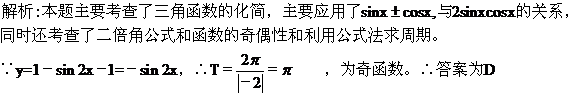 10.1919.(全国Ⅰ卷文9)为得到函数
10.1919.(全国Ⅰ卷文9)为得到函数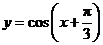 的图象,只需将函数
的图象,只需将函数 的图像( )
的图像( )
A.向左平移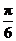 个长度单位 B.向右平移
个长度单位 B.向右平移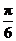 个长度单位
个长度单位
C.向左平移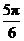 个长度单位 D.向右平移
个长度单位 D.向右平移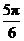 个长度单位
个长度单位

20.(全国Ⅱ卷理8)若动直线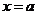 与函数
与函数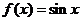 和
和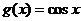 的图像分别交于
的图像分别交于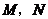 两点,则
两点,则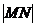 的最大值为( )
的最大值为( )
A.1 B.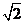 C.
C. D.2
D.2
[答案]B
[解析]在同一坐标系中作出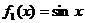 及
及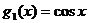 在
在 的图象,由图象知,当
的图象,由图象知,当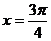 ,即
,即 时,得
时,得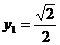 ,
,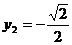 ,∴
,∴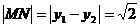
[高考考点]三角函数的图象,两点间的距离
[备考提示]函数图象问题是一个常考常新的问题
21.(全国Ⅱ卷文10)函数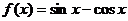 的最大值为( )
的最大值为( )
A.1 B.
 C.
C.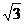 D.2
D.2
[答案]B
[解析]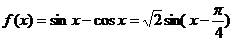 ,所以最大值是
,所以最大值是
[高考考点]三角函数中化为一个角的三角函数问题
[备考提示]三角函数中化为一个角的三角函数问题是三角函数在高考中的热点问题
22.(四川卷理10)设 ,其中
,其中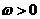 ,则
,则 是偶函数的充要条件是( )
是偶函数的充要条件是( )
(A)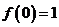 (B)
(B) (C)
(C)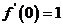 (D)
(D)
[解]:∵ 是偶函数
是偶函数
∴由函数 图象特征可知
图象特征可知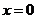 必是
必是 的极值点,
的极值点,
∴ 故选D
故选D
[点评]:此题重点考察正弦型函数的图象特征,函数的奇偶性,函数的极值点与函数导数的关系;
[突破]:画出函数图象草图,数形结合,利用图象的对称性以及偶函数图象关于 轴对称的要求,分析出
轴对称的要求,分析出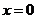 必是
必是 的极值点,从而
的极值点,从而 ;
;
23.(天津卷理3)设函数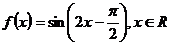 ,则
,则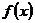 是
是
(A) 最小正周期为 的奇函数 (B) 最小正周期为
的奇函数 (B) 最小正周期为 的偶函数
的偶函数
(C) 最小正周期为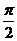 的奇函数 (D) 最小正周期为
的奇函数 (D) 最小正周期为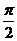 的偶函数
的偶函数
解析: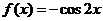 是周期为
是周期为 的偶函数,选B.
的偶函数,选B.
24.(天津卷理9)已知函数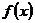 是R上的偶函数,且在区间
是R上的偶函数,且在区间 上是增函数.令
上是增函数.令 ,则
,则
(A) 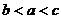 (B)
(B) 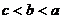 (C)
(C) 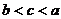 (D)
(D) 
解析: ,
,
因为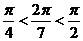 ,所以
,所以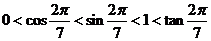 ,所以
,所以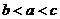 ,选A.
,选A.
25.(天津卷文6)把函数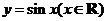 的图象上所有的点向左平行移动
的图象上所有的点向左平行移动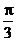 个单位长度,再把所得图象上所有点的横坐标缩短到原来的
个单位长度,再把所得图象上所有点的横坐标缩短到原来的 倍(纵坐标不变),得到的图象所表示的函数是( )
倍(纵坐标不变),得到的图象所表示的函数是( )
A.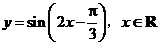 B.
B.
C.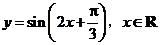 D.
D.
解析:选C,
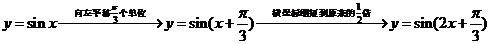 .
.
26.(天津卷文9)设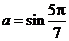 ,
, ,
, ,则( )
,则( )
A.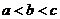 B.
B.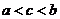 C.
C.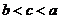 D.
D.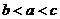
解析: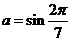 ,因为
,因为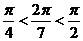 ,所以
,所以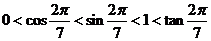 ,选D.
,选D.
27.(浙江卷理5文7)在同一平面直角坐标系中,函数 的图象和直线
的图象和直线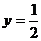 的交点个数是
的交点个数是
(A)0 (B)1 (C)2 (D)4
解析:本小题主要考查三角函数图像的性质问题。原函数可化为:
 =
=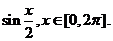 作出原函数图像,
作出原函数图像,
截取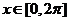 部分,其与直线
部分,其与直线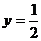 的交点个数是2个.
的交点个数是2个.
28.(浙江卷文2)函数 的最小正周期是
的最小正周期是
(A)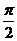 (B)
(B) (C)
(C)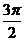 (D)
(D)
解析:本小题主要考查正弦函数周期的求解。原函数可化为: ,故其周期为
,故其周期为
29.(重庆卷理10)函数f(x)=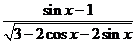 (
(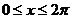 ) 的值域是
) 的值域是
(A)[- ] (B)[-1,0] (C)[-
] (B)[-1,0] (C)[-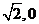 ] (D)[-
] (D)[-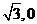 ]
]
解:特殊值法, 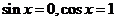 则f(x)=
则f(x)= 淘汰A,
淘汰A,
令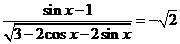 得
得 当时
当时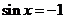 时
时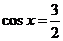 所以矛盾
所以矛盾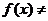
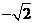 淘汰C,
D
淘汰C,
D
30.(重庆卷文12)函数f(x)=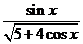 (0≤x≤2
(0≤x≤2 )的值域是
)的值域是
(A)[-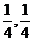 ] (B)[-
] (B)[-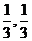 ] (C)[-
] (C)[-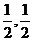 ]
(D)[-
]
(D)[-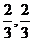 ]
]
[答案]C
[解析]本小题主要考查函数值域的求法。令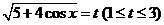 ,则
,则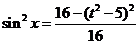 ,当
,当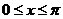 时,
时, ,
,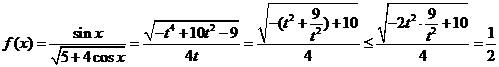 当且仅当
当且仅当 时取等号。同理可得当
时取等号。同理可得当 时,
时,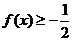 ,综上可知
,综上可知 的值域为
的值域为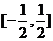 ,故选C。
,故选C。
1.(2009年广东卷文)(本小题满分12分)
已知向量 与
与 互相垂直,其中
互相垂直,其中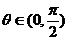
(1)求 和
和 的值
的值
(2)若 ,
,
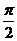 ,求
,求 的值
的值
[解析](1)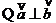 ,
, ,即
,即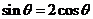
又∵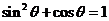 ,
∴
,
∴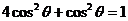 ,即
,即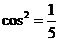 ,∴
,∴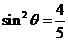
又  ,
,
(2) ∵
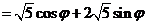
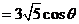
 ,
,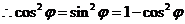 ,即
,即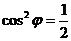
又 
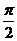 , ∴
, ∴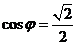


2.(2009全国卷Ⅰ理)(本小题满分10分)(注意:在试题卷上作答无效)
在 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为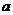 、
、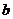 、
、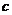 ,已知
,已知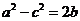 ,且
,且 求b
求b 

分析:此题事实上比较简单,但考生反应不知从何入手.对已知条件(1)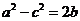 左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2)
左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2)  过多的关注两角和与差的正弦公式,甚至有的学生还想用现在已经不再考的积化和差,导致找不到突破口而失分.
过多的关注两角和与差的正弦公式,甚至有的学生还想用现在已经不再考的积化和差,导致找不到突破口而失分.
解法一:在 中
中 则由正弦定理及余弦定理有:
则由正弦定理及余弦定理有: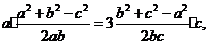 化简并整理得:
化简并整理得: .又由已知
.又由已知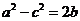
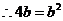 .解得
.解得 .
. 

解法二:由余弦定理得: 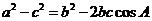 .又
.又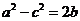 ,
, 。
。
所以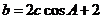 …………………………………①
…………………………………①
又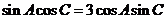 ,
,
 ,即
,即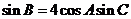
由正弦定理得 ,故
,故 ………………………②
………………………②
由①,②解得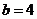 。
。
评析:从08年高考考纲中就明确提出要加强对正余弦定理的考查.在备考中应注意总结、提高自己对问题的分析和解决能力及对知识的灵活运用能力.另外提醒:两纲中明确不再考的知识和方法了解就行,不必强化训练。
3.(2009浙江理)(本题满分14分)在 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足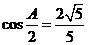 ,
,
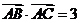 . (I)求
. (I)求 的面积; (II)若
的面积; (II)若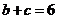 ,求
,求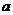 的值.
的值.
解析:(I)因为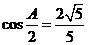 ,
, ,又由
,又由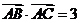 ,得
,得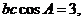
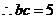 ,
,


(II)对于 ,又
,又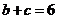 ,
,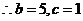 或
或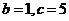 ,由余弦定理得
,由余弦定理得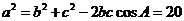 ,
,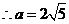


4.(2009浙江文)(本题满分14分)在 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足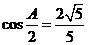 ,
,
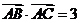 . (I)求
. (I)求 的面积; (II)若
的面积; (II)若 ,求
,求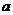 的值.
的值.
解析:(Ⅰ)


又 ,
, ,而
,而 ,所以
,所以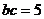 ,所以
,所以 的面积为:
的面积为: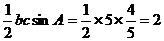
(Ⅱ)由(Ⅰ)知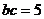 ,而
,而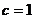 ,所以
,所以
所以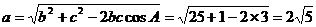
5.(2009北京文)(本小题共12分)已知函数 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
[解析]本题主要考查特殊角三角函数值、诱导公式、二倍角的正弦、三角函数在闭区间上的最值等基础知识,主要考查基本运算能力.
(Ⅰ)∵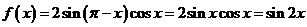 ,
,
∴函数 的最小正周期为
的最小正周期为 .
.
(Ⅱ)由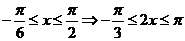 ,∴
,∴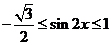 ,
,
∴ 在区间
在区间 上的最大值为1,最小值为
上的最大值为1,最小值为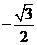 .
.
6.(2009北京理)(本小题共13分)
在 中,角
中,角 的对边分别为
的对边分别为 ,
,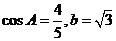 。
。
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的面积.
的面积.
[解析]本题主要考查三角形中的三角函数变换及求值、诱导公式、三角形的面积公式等基础知识,主要考查基本运算能力.
(Ⅰ)∵A、B、C为△ABC的内角,且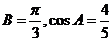 ,
,
∴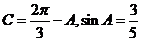 ,
,
∴ .
.
(Ⅱ)由(Ⅰ)知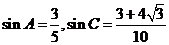 ,
,
又∵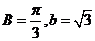 ,∴在△ABC中,由正弦定理,得
,∴在△ABC中,由正弦定理,得
∴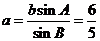 .
.
∴△ABC的面积 .
.
7.(2009江苏卷)(本小题满分14分)
设向量
(1)若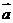 与
与 垂直,求
垂直,求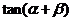 的值;
的值; 
(2)求 的最大值;
的最大值;
(3)若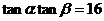 ,求证:
,求证: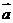 ∥
∥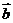 .
.

[解析] 本小题主要考查向量的基本概念,同时考查同角三角函数的基本关系式、二倍角的正弦、两角和的正弦与余弦公式,考查运算和证明得基本能力。满分14分。
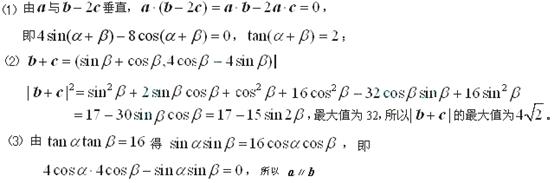
8.(2009山东卷理)(本小题满分12分)设函数f(x)=cos(2x+ )+sin
)+sin x.
x.
(1) 求函数f(x)的最大值和最小正周期.
(2) 设A,B,C为 ABC的三个内角,若cosB=
ABC的三个内角,若cosB=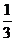 ,
,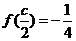 ,且C为锐角,求sinA.
,且C为锐角,求sinA.
解: (1)f(x)=cos(2x+ )+sin
)+sin x.=
x.=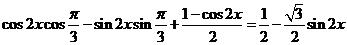
所以函数f(x)的最大值为 ,最小正周期
,最小正周期 .
. 

(2)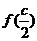 =
= =-
=-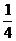 , 所以
, 所以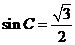 , 因为C为锐角, 所以
, 因为C为锐角, 所以 ,
,
又因为在 ABC 中, cosB=
ABC 中, cosB=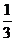 , 所以
, 所以 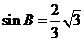 , 所以
, 所以 

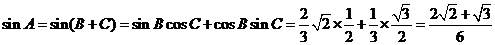 .
.
[命题立意]:本题主要考查三角函数中两角和差的弦函数公式、二倍角公式、三角函数的性质以及三角形中的三角关系.
9.(2009山东卷文)(本小题满分12分)设函数f(x)=2 在
在 处取最小值.
处取最小值.
(3)
求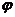 .的值;
.的值;
(4)
在 ABC中,
ABC中, 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知
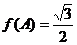 ,求角C..
,求角C..
解: (1)



因为函数f(x)在 处取最小值,所以
处取最小值,所以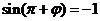 ,由诱导公式知
,由诱导公式知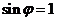 ,因为
,因为 ,所以
,所以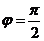 .所以
.所以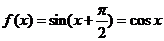


(2)因为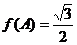 ,所以
,所以 ,因为角A为
,因为角A为 ABC的内角,所以
ABC的内角,所以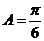 .又因为
.又因为 所以由正弦定理,得
所以由正弦定理,得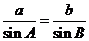 ,也就是
,也就是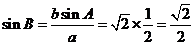 ,
,
因为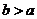 ,所以
,所以 或
或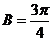 .
.
当 时,
时,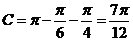 ;当
;当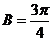 时,
时,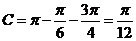 .
.
[命题立意]:本题主要考查了三角函数中两角和差的弦函数公式、二倍角公式和三角函数的性质,并利用正弦定理解得三角形中的边角.注意本题中的两种情况都符合.
10.(2009全国卷Ⅱ文)(本小题满分12分)设△ABC的内角A、B、C的对边长分别为a、b、c,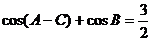 ,
,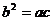 ,求B.
,求B.
解析:本题考查三角函数化简及解三角形的能力,关键是注意角的范围对角的三角函数值的制约,并利用正弦定理得到sinB=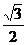 (负值舍掉),从而求出B=
(负值舍掉),从而求出B= 。
。
解:由 cos(A C)+cosB=
C)+cosB=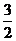 及B=π
及B=π (A+C)得
(A+C)得
cos(A C)
C) cos(A+C)=
cos(A+C)=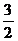 ,
,
cosAcosC+sinAsinC (cosAcosC
(cosAcosC sinAsinC)=
sinAsinC)=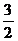 ,
,
sinAsinC=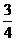 .
.
又由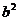 =ac及正弦定理得
=ac及正弦定理得 


故  ,
,
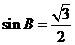 或
或 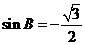 (舍去),
(舍去),
于是 B= 或 B=
或 B=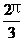 .
.
又由  知
知 或
或
所以 B= 。
。
11.(2009广东卷理)(本小题满分12分)
已知向量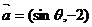 与
与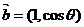 互相垂直,其中
互相垂直,其中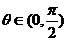 .
.
(1)求 和
和 的值;
的值;
(2)若 ,求
,求 的值.
的值.
解:(1)∵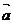 与
与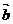 互相垂直,则
互相垂直,则 ,即
,即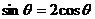 ,代入
,代入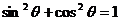 得
得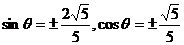 ,又
,又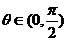 ,∴
,∴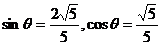 .
.
(2)∵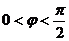 ,
,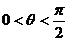 ,∴
,∴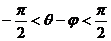 ,则
,则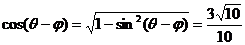 ,∴
,∴
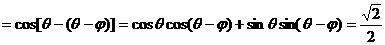 .
.
12.(2009安徽卷理)(本小题满分12分)
在 ABC中,
ABC中, , sinB=
, sinB= .
.
(I)求sinA的值;
(II)设AC= ,求
,求 ABC的面积.
ABC的面积.
本小题主要考查三角恒等变换、正弦定理、解三角形等有关知识,考查运算求解能力。本小题满分12分
解:(Ⅰ)由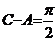 ,且
,且 ,∴
,∴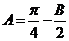 ,∴
,∴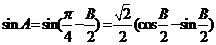 ,
,
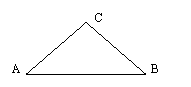 ∴
∴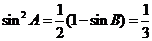 ,又
,又 ,∴
,∴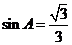
(Ⅱ)如图,由正弦定理得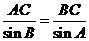
∴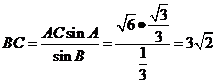 ,又
,又
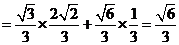
∴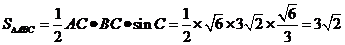


13.(2009安徽卷文)(本小题满分12分)
在 ABC中,C-A=
ABC中,C-A= ,
sinB=
,
sinB=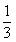 。
。
(I)求sinA的值;
(II)设AC=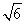 ,求
,求 ABC的面积。
ABC的面积。
[思路](1)依据三角函数恒等变形可得关于 的式子,这之中要运用到倍角公式;
的式子,这之中要运用到倍角公式;
(2)应用正弦定理可得出边长,进而用面积公式可求出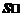 .
.
[解析](1)∵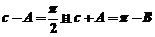 ∴
∴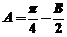 ∴
∴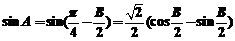 w.w.w.k.s.5.u.c.o.∴
w.w.w.k.s.5.u.c.o.∴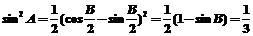 又
又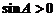 ∴
∴
(2)如图,由正弦定理得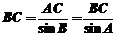 ∴
∴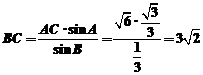
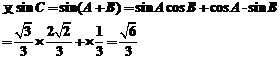
∴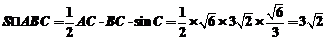 .
. 

14.(2009江西卷文)(本小题满分12分)在△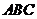 中,
中,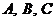 所对的边分别为
所对的边分别为 ,
,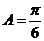 ,
,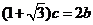 .(1)求
.(1)求 ;(2)若
;(2)若 ,求
,求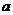 ,
,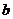 ,
,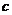 .
.
解:(1)由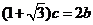 得
得

则有 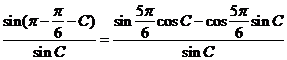 =
=
得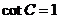 即
即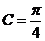 .
.
(2) 由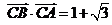 推出
推出
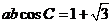 ;而
;而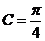 ,
,
即得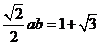 , 则有
, 则有
 解得
解得 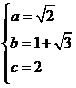
15.(2009江西卷理)(本小题满分12分)△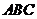 中,
中,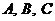 所对的边分别为
所对的边分别为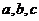 ,
,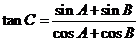 ,
, .(1)求
.(1)求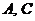 ;(2)若
;(2)若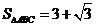 ,求
,求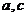 . w.
. w.
解:(1) 因为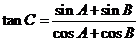 ,即
,即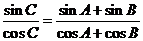 ,
,
所以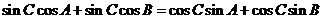 ,
,
即  ,
,
得
 . 所以
. 所以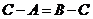 ,或
,或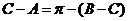 (不成立).
(不成立).
即 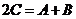 , 得
, 得 ,所以.
,所以.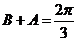
又因为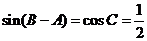 ,则
,则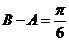 ,或
,或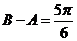 (舍去)
得
(舍去)
得
(2)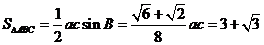 ,
,
又 , 即
, 即  ,得
,得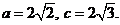
16.(2009天津卷文)(本小题满分12分)在 中,
中,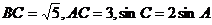
(Ⅰ)求AB的值。(Ⅱ)求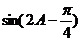 的值。
的值。
[解析](1)解:在 中,根据正弦定理,
中,根据正弦定理, ,于是
,于是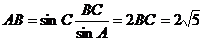
(2)解:在 中,根据余弦定理,得
中,根据余弦定理,得
于是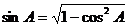 =
=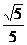 ,从而
,从而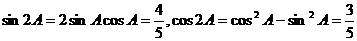

[考点定位]本题主要考查正弦定理,余弦定理同角的三角函数的关系式,二倍角的正弦和余弦,两角差的正弦等基础知识,考查基本运算能力。
17.(2009四川卷文)(本小题满分12分)在 中,
中,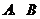 为锐角,角
为锐角,角 所对的边分别为
所对的边分别为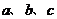 ,且
,且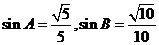 (I)求
(I)求 的值;(II)若
的值;(II)若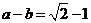 ,求
,求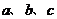 的值。
的值。
[解析](I)∵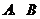 为锐角,
为锐角,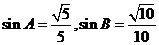
∴ 
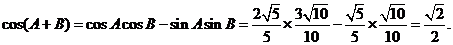
∵  ∴
∴ 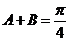 …6分
…6分
(II)由(I)知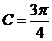 ,∴
,∴ 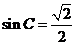 由
由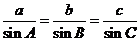 得
得
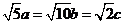 ,即
,即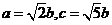 又∵
又∵ 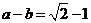
∴ 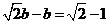 ∴
∴ 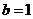 ∴
∴  …12分
…12分
18.(2009全国卷Ⅱ理)(本小题满分10分)设 的内角
的内角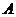 、
、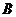 、
、 的对边长分别为
的对边长分别为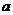 、
、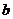 、
、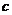 ,
,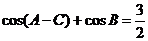 ,
, ,求
,求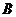 。
。
分析:由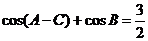 ,易想到先将
,易想到先将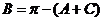 代入
代入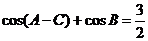 得
得 。然后利用两角和与差的余弦公式展开得
。然后利用两角和与差的余弦公式展开得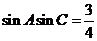 ;又由
;又由 ,利用正弦定理进行边角互化,得
,利用正弦定理进行边角互化,得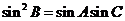 ,进而得
,进而得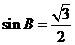 .故
.故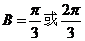 。大部分考生做到这里忽略了检验,事实上,当
。大部分考生做到这里忽略了检验,事实上,当 时,由
时,由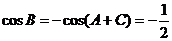 ,进而得
,进而得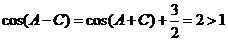 ,矛盾,应舍去。
,矛盾,应舍去。
也可利用若 则
则 从而舍去
从而舍去 。不过这种方法学生不易想到。
。不过这种方法学生不易想到。
评析:本小题考生得分易,但得满分难。
19.(2009湖南卷文)(每小题满分12分)
已知向量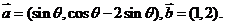
(Ⅰ)若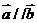 ,求
,求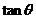 的值;(Ⅱ)若
的值;(Ⅱ)若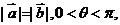 求
求 的值。
的值。
解:(Ⅰ) 因为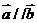 ,所以
,所以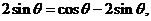 于是
于是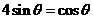 ,故
,故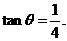
(Ⅱ)由 知,
知,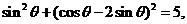 所以
所以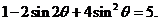
从而 ,即
,即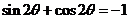 ,
,
于是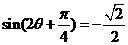 .又由
.又由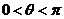 知,
知, ,
,
所以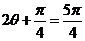 ,或
,或 .因此
.因此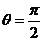 ,或
,或
20.(2009福建卷理)(本小题满分13分)如图,某市拟在长为8km的道路OP的一侧修建一条运动
 赛道,赛道的前一部分为曲线段OSM,该曲线段为函数
赛道,赛道的前一部分为曲线段OSM,该曲线段为函数
y=Asin x(A>0,
x(A>0,  >0) x
>0) x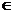 [0,4]的图象,且图象的最高点为
[0,4]的图象,且图象的最高点为
S(3,2 );赛道的后一部分为折线段MNP,为保证参赛
);赛道的后一部分为折线段MNP,为保证参赛
运动员的安全,限定 MNP=120
MNP=120 (I)求A ,
(I)求A ,  的值和M,P两点间的距离;(II)应如何设计,才能使折线段赛道MNP最长?
的值和M,P两点间的距离;(II)应如何设计,才能使折线段赛道MNP最长? 

18.本小题主要考查三角函数的图象与性质、解三角形等基础知识,考查运算求解能力以及应用数学知识分析和解决实际问题的能力,考查化归与转化思想、数形结合思想,
解法一
(Ⅰ)依题意,有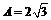 ,
,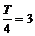 ,又
,又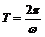 ,
,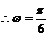 。
。
当 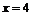 是,
是,
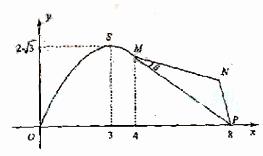
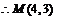 又
又

(Ⅱ)在△MNP中∠MNP=120°,MP=5,
设∠PMN= ,则0°<
,则0°< <60°
<60°
由正弦定理得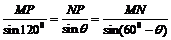
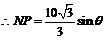 ,
,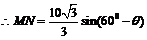
故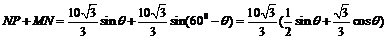

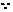 0°<
0°< <60°,
<60°, 当
当 =30°时,折线段赛道MNP最长
=30°时,折线段赛道MNP最长
亦即,将∠PMN设计为30°时,折线段道MNP最长
解法二:
(Ⅰ)同解法一
(Ⅱ)在△MNP中,∠MNP=120°,MP=5,由余弦定理得 ∠MNP=
∠MNP=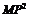
即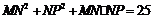 故
故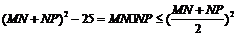
从而 ,即
,即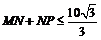 当且仅当
当且仅当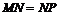 时,折线段道MNP最长
时,折线段道MNP最长
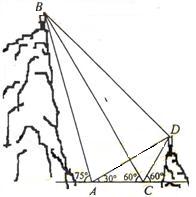 注:本题第(Ⅱ)问答案及其呈现方式均不唯一,除了解法一、解法二给出的两种设计方式,还可以设计为:①
注:本题第(Ⅱ)问答案及其呈现方式均不唯一,除了解法一、解法二给出的两种设计方式,还可以设计为:① ;②
;② ;③点N在线段MP的垂直平分线上等
;③点N在线段MP的垂直平分线上等
21.(2009辽宁卷文)(本小题满分12分)
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为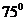 ,
, ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为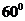 ,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km,
,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km,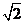
 1.414,
1.414,
 2.449)
2.449) 

(18)解: 在 中,
中,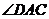 =30°,
=30°, =60°-
=60°-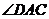 =30°,
=30°,
所以CD=AC=0.1 又 =180°-60°-60°=60°,
=180°-60°-60°=60°,
故CB是 底边AD的中垂线,所以BD=BA 5分
底边AD的中垂线,所以BD=BA 5分
在 中,
中,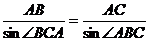 , 即AB=
, 即AB=
因此, 故B、D的距离约为0.33km。12分
故B、D的距离约为0.33km。12分
22.(2009辽宁卷理)(本小题满分12分)
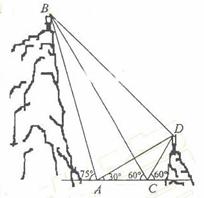 如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为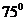 ,
, ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为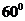 ,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,
,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,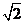
 1.414,
1.414,
 2.449)
2.449) 

(17)解:
在△ABC中,∠DAC=30°, ∠ADC=60°-∠DAC=30,
所以CD=AC=0.1 又∠BCD=180°-60°-60°=60°,
故CB是△CAD底边AD的中垂线,所以BD=BA, ……5分
在△ABC中,
即AB=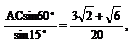
因此,BD=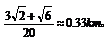 故B,D的距离约为0.33km。…12分
故B,D的距离约为0.33km。…12分
23.(2009宁夏海南卷理)(本小题满分12分)为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N
14.(2009辽宁卷文)已知函数 的图象如图所示,
的图象如图所示, 

则 =
=
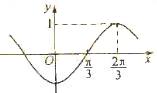
[解析]由图象可得最小正周期为
∴T= Þ ω=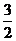
[答案]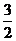
13.(2009湖北卷理)已知函数 则
则 的值为 .
的值为 .
[答案]1
[解析]因为 所以
所以
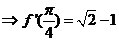 故
故
12.(2009上海卷文)已知函数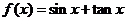 。项数为27的等差数列
。项数为27的等差数列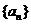 满足
满足 且公差
且公差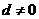 ,若
,若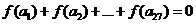 ,则当k=
时,
,则当k=
时,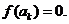 。
。
[答案]14
[解析]函数 在
在  是增函数,显然又为奇函数,函数图象关于原点对称,因为
是增函数,显然又为奇函数,函数图象关于原点对称,因为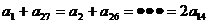 ,
, 

所以 ,所以当
,所以当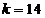 时,
时, .
.
11.(2009上海卷文)函数 的最小值是
。
的最小值是
。
[答案]
[解析]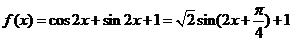 ,所以最小值为:
,所以最小值为:
10.(2009年上海卷理)已知函数 .项数为27的等差数列
.项数为27的等差数列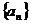 满足
满足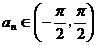 ,且公差
,且公差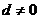 .若
.若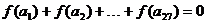 ,则当
,则当 =____________是,
=____________是, .
.
[答案]14
[解析]函数 在
在  是增函数,显然又为奇函数,函数图象关于原点对称,因为
是增函数,显然又为奇函数,函数图象关于原点对称,因为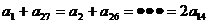 ,
,
所以 ,所以当
,所以当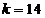 时,
时, .
.
9.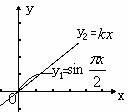 .(2009年上海卷理)当
.(2009年上海卷理)当 ,不等式
,不等式 成立,则实数
成立,则实数 的取值范围是_______________.
的取值范围是_______________.
[答案]k≤1
[解析]作出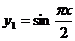 与
与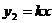 的图象,要使不等式
的图象,要使不等式 成立,由图可知须k≤1。
成立,由图可知须k≤1。
8. (2009年上海卷理)在极坐标系中,由三条直线
(2009年上海卷理)在极坐标系中,由三条直线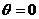 ,
, ,
, 围成图形的面积是________.
围成图形的面积是________. 

[答案]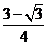


[解析]化为普通方程,分别为:y=0,y=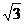 x,x+y=1,画出三条直线的图象如右图,可求得A(
x,x+y=1,画出三条直线的图象如右图,可求得A( ,
,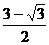 ),B(1,0),三角形AOB的面积为:
),B(1,0),三角形AOB的面积为: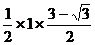 =
=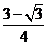
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com