
18.(金华十校2009年3月高考模拟试卷)已知函数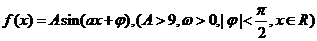 的图象的一部分如下图所示。(1)求函数
的图象的一部分如下图所示。(1)求函数 的解析式;(2)当
的解析式;(2)当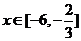 时,求函数
时,求函数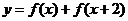 的最大值与最小值及相应的
的最大值与最小值及相应的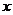 的值。
的值。
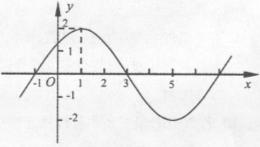
解:(1)由图像知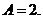
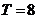 ,
,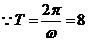 ,
,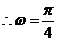 ,又图象经过点(-1,0)
,又图象经过点(-1,0)
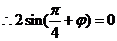
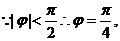

(2)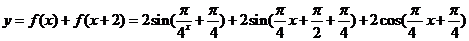
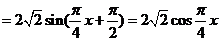
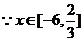 ,
, 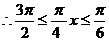
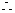 当
当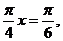 即
即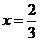 时,
时,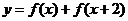 的最大值为
的最大值为 ,当
,当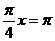 , 即
, 即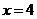 时, 最小值为
时, 最小值为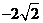
[一年原创] 2008和2009原创试题及其解析
17.(2009届山东省实验中学第四次测试)已知函数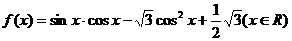 .(1)求
.(1)求 的最小正周期;(2)求
的最小正周期;(2)求 的单调递增区间;(3)求
的单调递增区间;(3)求 图象的对称轴方程和对称中心的坐标.
图象的对称轴方程和对称中心的坐标.
解: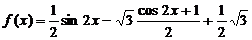 =
=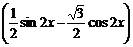 =
=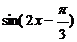
(1)T=π;
(2)由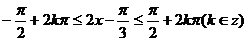
可得单调增区间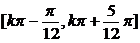 (
(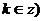 .
.
(3)由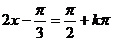 得对称轴方程为
得对称轴方程为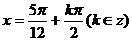 ,
,
由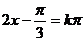 得对称中心坐标为
得对称中心坐标为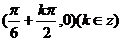 .
.
16.(福州市2009年高中毕业班质量检查)已知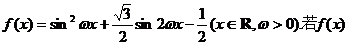 的最小正周期为
的最小正周期为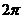 。(I)求
。(I)求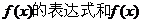 的单调递增区间; (II)求
的单调递增区间; (II)求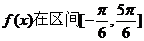 的最大值和最小值
的最大值和最小值
解:(I)由已知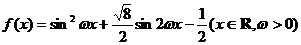
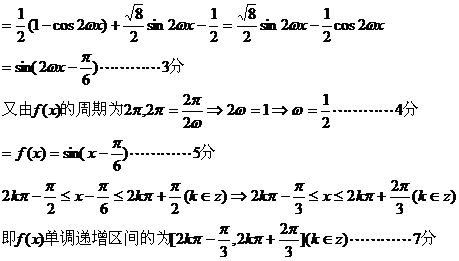
(II)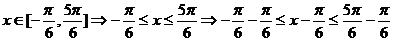
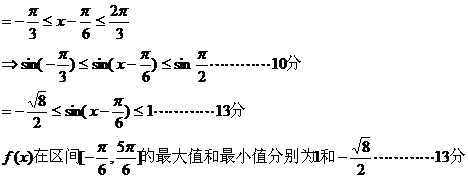
15.(2009玉溪一中期中)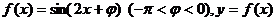 图像的一条对称轴是直线
图像的一条对称轴是直线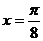 。
。
(Ⅰ)求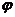 ;(Ⅱ)画出函数
;(Ⅱ)画出函数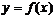 在区间
在区间 上的图像。
上的图像。
解:(Ⅰ) 的图像的对称轴,
的图像的对称轴,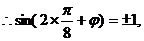
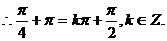
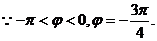
(Ⅱ)由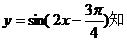
|
x |
0 |
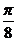 |
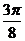 |
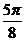 |
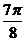 |
 |
|
y |
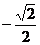 |
-1 |
0 |
1 |
0 |
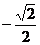 |
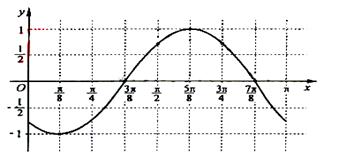 故函数
故函数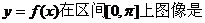
14.(2009玉溪市民族中学第四次月考)已知函数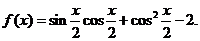
(Ⅰ)将函数 化简成
化简成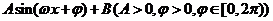 的形式,并指出
的形式,并指出 的最小正周期;
的最小正周期;
(Ⅱ)求函数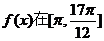 上的最大值和最小值
上的最大值和最小值
解 (Ⅰ) f(x)= sinx+
sinx+ .
.
故f(x)的最小正周期为2π{k∈Z且k≠0}。
(Ⅱ)由π≤x≤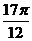 ,得
,得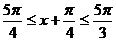 .因为f(x)=
.因为f(x)=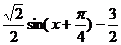 在
在
[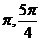 ]上是减函数,在[
]上是减函数,在[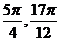 ]上是增函数,故当x=
]上是增函数,故当x=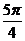 时,f(x)有最小值-
时,f(x)有最小值-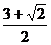 ;而f(π)=-2,f(
;而f(π)=-2,f(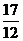 π)=-
π)=-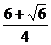 <-2,所以当x=π时,f(x)有最大值-2.
<-2,所以当x=π时,f(x)有最大值-2.
13.(山东省聊城市2009 年 高 考 模 拟 试 题)设函数 。
。
(1)写出函数 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)当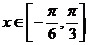 时,函数
时,函数 的最大值与最小值的和为
的最大值与最小值的和为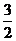 ,求a的值。
,求a的值。
解(1)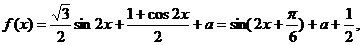
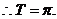
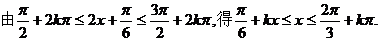
故函数 的单调递减区间是
的单调递减区间是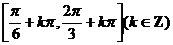 。
。
|
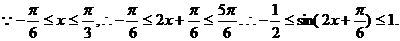
当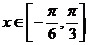 时,原函数的最大值与最小值的和
时,原函数的最大值与最小值的和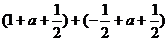
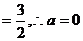
11.(2009上海奉贤区模拟考)已知函数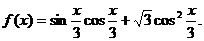 (1)将
(1)将 写成
写成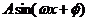 的形式,并求其图象对称中心的横坐标;(2)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为
的形式,并求其图象对称中心的横坐标;(2)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为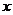 ,试求角
,试求角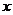 的范围及此时函数
的范围及此时函数 的值域.
的值域.
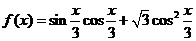 =
=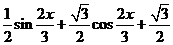 =
=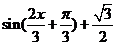
若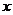 为其图象对称中心的横坐标,即
为其图象对称中心的横坐标,即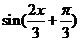 =0,
=0, 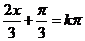 , 解得:
, 解得: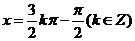
(2)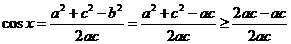 ,
,
即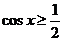 ,而
,而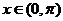 ,所以
,所以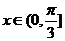 。
。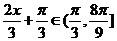 ,
,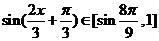 ,
,
所以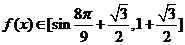
12(安徽合肥2009模拟)已知函数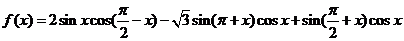
(1)求函数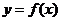 的最小正周期和最值;(2)指出
的最小正周期和最值;(2)指出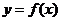 图像经过怎样的平移变换后得到的图像关于原点对称。
图像经过怎样的平移变换后得到的图像关于原点对称。
.解:(1)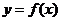 最小正周期
最小正周期
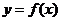 的最大值为
的最大值为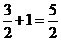 ,最小值为
,最小值为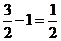 ………6分
………6分
(2),∵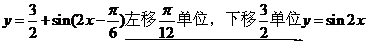
10.(2009长郡中学第六次月考)已知函数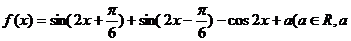 为常数).
为常数). (1)求函数
(1)求函数 的最小正周期;(2)求函数
的最小正周期;(2)求函数 的单调递增区间;(3) 若
的单调递增区间;(3) 若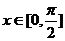 时,
时, 的最小值为
的最小值为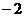 ,求
,求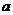 的值.
的值.
解:(1) 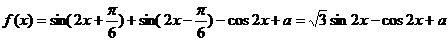
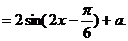
∴ 的最小正周期
的最小正周期 .
.
(2) 当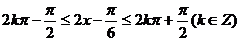 ,
,
即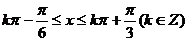 时,函数
时,函数 单调递增,
单调递增,
故所求区间为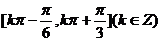
(3) 当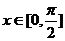 时,
时,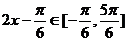 ∴当
∴当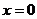 时
时 取得最小值,
取得最小值,
即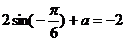 , ∴
, ∴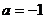 .
.
9.(2009枣庄一模)已知函数
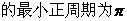 (1)求
(1)求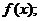 (2)当
(2)当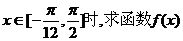 的值域。
的值域。
解:(1)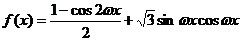
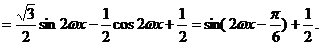
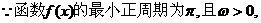
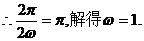
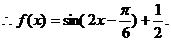
(2)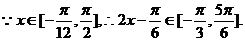
根据正弦函数的图象可得: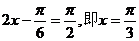 时,
时,
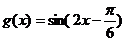 取最大值1 当
取最大值1 当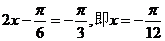 时
时
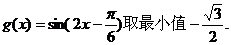
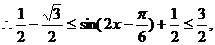
8.(2009福州三中)已知 , f(x)=
, f(x)=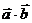 。
。
(1)求函数在[0,p]上的单调增区间;(2)当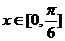 时,f(x)的最大值为4,求实数m的值。
时,f(x)的最大值为4,求实数m的值。
|
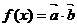
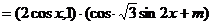
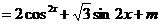
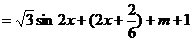 令
令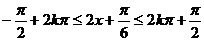
得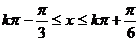
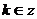
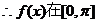 上的单调增区间为
上的单调增区间为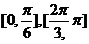
(2)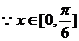
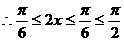
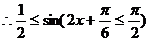
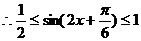
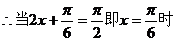
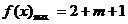 依题意得:
依题意得: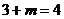
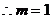
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com