
2.证明三角等式的思路和方法。(1)思路:利用三角公式进行化名,化角,改变运算结构,使等式两边化为同一形式。(2)证明方法:综合法、分析法、比较法、代换法、相消法、数学归纳法。
1.三角函数恒等变形的基本策略。(1)注意隐含条件的应用:1=cos2x+sin2x。(2)角的配凑。α=(α+β)-β,β=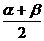 -
-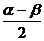 等。(3)升幂与降幂。主要用2倍角的余弦。(4)化弦(切)法,用正弦定理或余弦定理。(5)引入辅助角。asinθ+bcosθ=
等。(3)升幂与降幂。主要用2倍角的余弦。(4)化弦(切)法,用正弦定理或余弦定理。(5)引入辅助角。asinθ+bcosθ=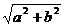 sin(θ+
sin(θ+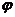 ),这里辅助角
),这里辅助角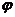 所在象限由a、b的符号确定,
所在象限由a、b的符号确定,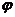 角的值由tan
角的值由tan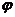 =
= 确定。
确定。
13.(1)已知 为锐角,且
为锐角,且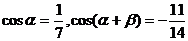 ,求
,求 ;
;
(2)已知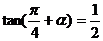 ,求
,求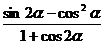 的值.
的值.
答案:(1)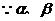 为锐角,且
为锐角,且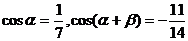
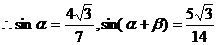 …………………… 2分
…………………… 2分
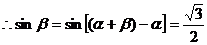 …………………… 4分
…………………… 4分
又 为锐角,故
为锐角,故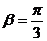 ……………6分
……………6分
(2)
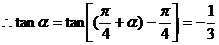 …
3分
…
3分
则 …………6分
…………6分
[考点预测] 2010高考预测
12.已知函数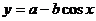 (b>0)的最大值是
(b>0)的最大值是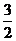 ,最小值是
,最小值是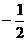 ,求函数
,求函数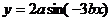 的最小正周期、振幅和单调区间.
的最小正周期、振幅和单调区间.
答案:(12分)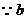 >0,
>0,
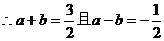 2分
2分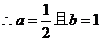 ………… 3分
………… 3分
则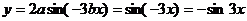 … 4分
… 4分
故最小正周期为 … 6分振幅为1
8分
… 6分振幅为1
8分
由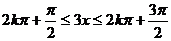 的增区间为
的增区间为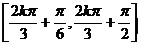 … 10分
… 10分
同理可得减区间为 ……………………12分
……………………12分
11.在△ABC中,tanA=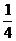 ,tanB=
,tanB=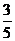 . (1)求角C的大小; (2)若AB边的长为
. (1)求角C的大小; (2)若AB边的长为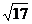 ,求BC边的长.
,求BC边的长.
答案:解:(Ⅰ) ,
,
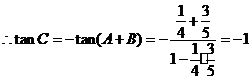 .又
.又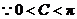 ,
, .(6分)
.(6分)
(Ⅱ)由 且
且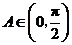 ,
,
得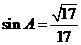 .
. ,
, .(6分)
.(6分)
10.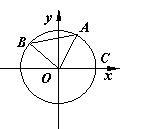 如图
如图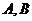 是单位圆
是单位圆 上的动点,且
上的动点,且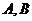 分别在第一,二象限.
分别在第一,二象限.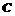 是圆与
是圆与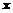 轴正半轴的交点,
轴正半轴的交点,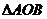 为正三角形. 若
为正三角形. 若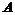 点的坐标为
点的坐标为 . 记
. 记 .
.
(Ⅰ)若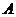 点的坐标为
点的坐标为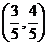 ,求
,求 的值;
的值;
(Ⅱ)求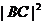 的取值范围.
的取值范围.
解:(1)因为A点的坐标为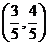 ,根据三角函数定义可知,
,根据三角函数定义可知, ,得
,得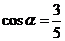 ,.
,.
所以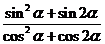 =
=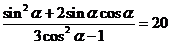 ....6分
....6分
(Ⅱ)因为三角形AOB为正三角形,所以 ,
,
所以 =
= =
= .......7分
.......7分
所以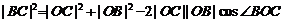 =
= .....................8分
.....................8分
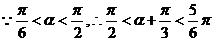 ,
,
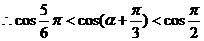 ,
,
即 ,...10分
,...10分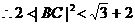 ..12分
..12分
9.在△ABC中,角A、B、C所对的边分别为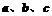 ,已知
,已知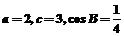 ,(1)求
,(1)求 的值;(2)求
的值;(2)求 的值.
的值.
解:(1)由余弦定理,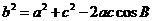 2分得
2分得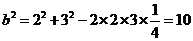 , 4分
, 4分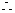
 .…6分
.…6分
(2)方法1:由余弦定理,得 ,
,  ,…10分
,…10分
∵ 是
是 的内角,∴
的内角,∴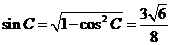 .……12分
.……12分
方法2:∵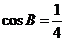 ,且
,且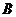 是
是 的内角,∴
的内角,∴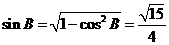 .………8分
.………8分
根据正弦定理,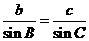 ,… 10分得
,… 10分得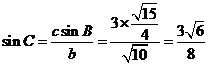 .……12分
.……12分
8.已知向量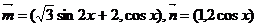 ,设函数
,设函数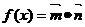 。
。
(1)求 的最小正周期与单调递减区间。(2)在
的最小正周期与单调递减区间。(2)在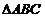 中,
中,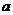 、
、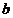 、
、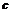 分别是角
分别是角 、
、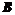 、
、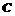 的对边,若
的对边,若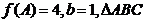 的面积为
的面积为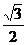 ,求
,求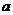 的值。
的值。
解:(Ⅰ)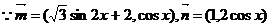 ,
,

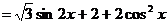
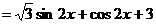
 .3分
.3分 ………4分
………4分
令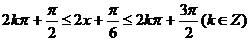
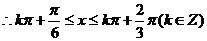
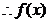 的单调区间为
的单调区间为 ,k∈Z ...............6分
,k∈Z ...............6分
(Ⅱ)由 得
得 
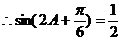 ...................7分
...................7分
又 为
为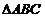 的内角
的内角 

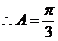 ..................9分
..................9分
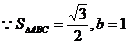
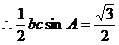
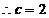 .............10分
.............10分
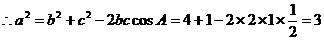
 ..............12分
..............12分
7.已知函数 .
.
(Ⅰ)若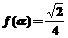 ,
,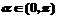 ,求
,求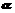 的值;
的值;
(Ⅱ)求函数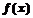 在
在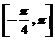 上最大值和最小值.
上最大值和最小值.
答案:
|
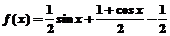

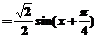
由题意知 
即 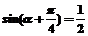
∵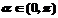 即
即 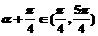
∴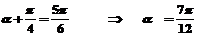
(2)∵  即
即 
∴ ,
, 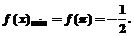
6、已知函数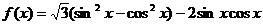 .
.
(Ⅰ)求 的最小正周期;(Ⅱ)设
的最小正周期;(Ⅱ)设 ,求
,求 的值域和单调递增区间.学科
的值域和单调递增区间.学科
网[解](Ⅰ)∵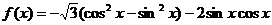

 . … 3分
. … 3分 的最小正周期为
的最小正周期为 . …… 5分
. …… 5分
(Ⅱ)∵ ,
,  ,
, 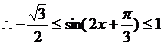 .
.
 的值域为
的值域为 .……… 10分
.……… 10分
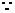 当
当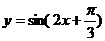 递减时,
递减时, 递增.
递增.
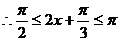 ,即
,即 .
.
故 的递增区间为
的递增区间为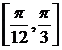 .…………12分
.…………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com