
3、若 两两互相垂直,
两两互相垂直,
求证: 为锐角三角形。
为锐角三角形。
2、已知 是空间两个单位向量,它们的夹角是
是空间两个单位向量,它们的夹角是 ,设向量
,设向量
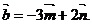
(1)求 (2)求
(2)求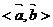
1、在空间四边形ABCD中,AB⊥CD,AC⊥BD,求证:AD⊥BC
例1.在正四面体ABCD中,棱长为1,点E,F分别为AB,AD的中点。
求:(1)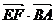 ,(2)
,(2)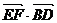 ,
,
(3) ,(4)
,(4)
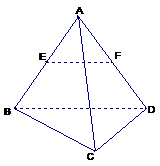

例2.已知四棱柱 的底面
的底面 是矩形,
是矩形,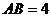 ,
, ,
,  ,
, 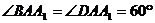 ,
,
求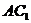 的长。
的长。
例3.已知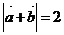 ,
, ,且
,且 ,则
,则 _______,
_______,
 _________.
_________.
例4. 已知空间四边形 中,
中,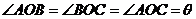 ,且
,且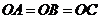 ,
,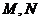 分别是
分别是 的中点,
的中点, 是
是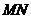 的中点,求证:
的中点,求证: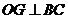

 例5、在正四面体
例5、在正四面体 中,点
中,点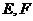 分别为
分别为 的中点,求异面直线
的中点,求异面直线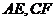 所成角的余弦值。
所成角的余弦值。
2、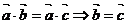 对吗?
对吗?
理由:
 对吗?
对吗?
理由:
①、两个向量的夹角的定义:
__________________________________________________________________________
图形:
◆注意点:
1)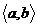 的范围:______________
的范围:______________
2)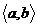 与
与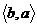 相等吗?__________
相等吗?__________
3)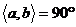 时,则称_______,记作______
时,则称_______,记作______
②、两个向量的数量积定义:
__________________________________________________________________________
◆注意点:
1)两个向量的数量积是数量还是向量?
_____________________________________
2)规定:零向量与任意向量的数量积为____
思考: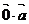 是零向量吗?
是零向量吗? 是零向量吗?
是零向量吗?
_____________________________________
◆总结:对于非零向量 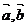 ,有:
,有:
1)  ___________________
___________________
 2)
2)  ______________
______________
3) 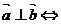 ________
________
4) 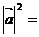 ___________
___________
③、空间向量的数量积满足的运算律
1)______________________
2)______________________
3)______________________
◆注意点:
1、数量积满足结合律吗?
理由:
4.E,F,G,H分别为正方体ABCD-A1B1C1D1的棱A1B1,A1D1,B1C1,C1D1的中点.
求证:(1)E,F,D,B四点共面;
(2)平面AEF∥平面BDHG.
[问题反馈]
3.三棱锥O-ABC中,G,H分别是△ABC,
△OBC的重心,设
试用向量 表示向量
表示向量
2.平行六面体ABCD-A’B’C’D’中,
求证:
1.已知 是不共面的三个向量,若它们的起点相同,且
是不共面的三个向量,若它们的起点相同,且 及
及 的终点共面,则实数t=_______
的终点共面,则实数t=_______
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com