2.光的干涉和衍射

⑴光的干涉现象和衍射现象证明了光的波动性，光的偏振现象说明光波为横波。相邻亮条纹(或相邻暗条纹)之间的间距(相邻亮条纹中央间距，相邻暗条纹中央间距)为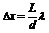。利用双缝干涉实验可以测量光的波长。

⑵干涉和衍射的产生条件

①光屏上出现亮条纹(或暗条纹)的条件：

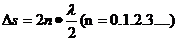亮条纹： 暗条纹：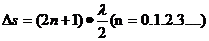

②发生明显衍射的条件：障碍物或孔的尺寸与光波波长可比(相差不多)

1. 折射率和全反射

(1)折射率(绝对折射率n)光从真空射入某种介质发生折射时,入射角θ₁的正弦与折射角θ₂的正弦之比n,叫做这种介质的折射率,即。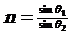

(2)临界角：折射角等于90⁰时的入射角叫临界角．显然，临界角是一种特殊的入射角．当光线从某介质射入真空(或空气)时，其临界角的正弦值为．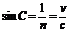

注意：发生反射时，不一定发生折射，如：全反射时无折射；发生折射时，却一定存在反射。

(3)产生全反射的条件是：

①光从光密介质射向光疏介质；

②入射角大于或等于临界角．两条件必须同时存在，才发生全反射。

23．(本题满分18分，共3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分)

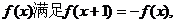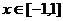定义在R上的偶函数且当时，。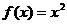

　 (1)求证：2是函数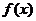的一个周期；

　 (2)求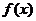在区间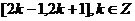上的函数解析式；

　 (3)是否存在整数k，使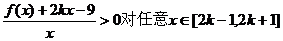恒成立？若存在，请求出k的取值范围；若不存在，请说明理由.

22．(本题满分18分)第(1)题4分，第(2)题5分，第(3)题9分。

已知函数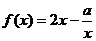的定义域为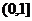(a为实数)。

　 (1)当a= -1时，求函数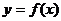的值域；

　 (2)当a>0时，判断函数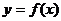的单调性并给予证明；

　 (3)求函数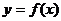在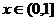上的最大值及最小值，并求出函数取最值时x的值。

21．(本题满分15分，本题共2个小题，第1小题满分6分，第2小题满分9分)

某种出口产品的关税税率t、市场价格x(单位：千元)与市场供应量p(单位：万件)之间近似满足关系式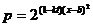：，其中k，b均为常数。当关税税率为75%时，若市场价格为5千元，则市场供应量约为1万件；若市场价格为7千元，则市场供应量约为2万件。

　 (1)试确定k、b的值；

　 (2)市场需求量q(单位：万件)与市场价格x近似满足关系式：q=2^-x.当p=q时，市场价格称为市场平衡价格。当市场平衡价格不超过4千元时，试确定关税税率的最大值。

20．(本题满分15分，第(1)题7分，第(2)题8分)

已知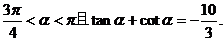

(1)求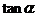的值；

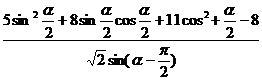(2)求的值.

19．(本题满分12分)

已知全集为R，集合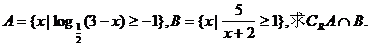

18．设定义域为R的函数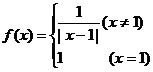，若关于x的方程 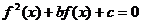三个不同的实数解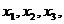则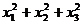等于　　　　　　　　　　　　　　　　　　　 (　　 )

　　 A．5　　　　　　　　　　　　　　 B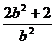．　　　　　 C．11　　　　　　　　　　　　 D．3

16．若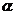为第二象限角，则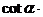

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

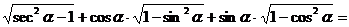
　　　 A．0　　　　　　　　　　　　 B．2　　　　　　　　　　　 C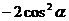．　　　　　 D．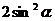

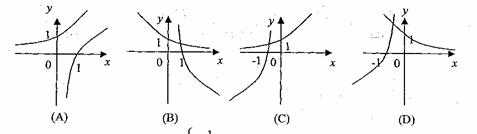　 17．已知a>0且a≠1，函数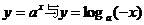的图像只可能是　　　　　　　　　　　 (　　 )