
例1、已知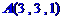 、
、 ,求:
,求:
(1)线段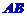 的中点坐标和长度;
的中点坐标和长度;
(2)到 两点距离相等的点 的
两点距离相等的点 的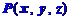 坐标
坐标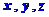 满足的条件。
满足的条件。
(1)M AB=
AB=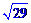
(2) 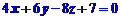
练:写出与点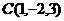 距离等于4的点
距离等于4的点 的坐标
的坐标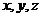 满足的关系式。
满足的关系式。

例2、若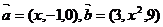 的夹角为钝角,求实数
的夹角为钝角,求实数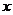 的取值范围。
的取值范围。

例3、在正方体 中,
中,  分别为
分别为 的中点.
的中点.
(1)求 与
与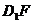 所成的角;
所成的角;

 (2)证明:
(2)证明: 面
面
④、(链接)射影
定义:
新知见课件___________________________
提问: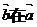 方向上的投影:
方向上的投影:
3、已知向量 满足
满足
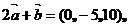
 且
且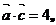 求
求

2、已知向量
求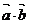 ,
, 及
及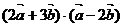


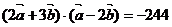
1、 则
则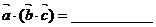 ,
,


◆该题说明什么结论:数量积不满足结合律
①、数量积的坐标形式:
新知见课件___________________________
_____________________________________
②、距离的坐标形式:
1)、 向量的长度(模)公式:
新知见课件___________________________
2)、空间两点的距离公式
新知见课件___________________________
_____________________________________
③、夹角的坐标表示:
新知见课件___________________________
_____________________________________
◆思考:当 及
及 时,夹角分别在什么范围内?
时,夹角分别在什么范围内?
新知见课件___________________________
4、已知 的三个顶点
的三个顶点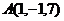 ,
,
 ,
,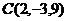 .
.
(1)试求 的各边长;(2)求
的各边长;(2)求 的三个内角的大小;(3)写出
的三个内角的大小;(3)写出 的重心坐标及外心坐标。
的重心坐标及外心坐标。
3、已知点 的坐标分别为
的坐标分别为 ,
,
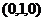 ,
,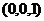 。求满足下列条件的点
。求满足下列条件的点 的坐标:(1)
的坐标:(1)
(2)  且
且
2、若 且
且 ,则
,则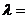 __________
__________
1、与向量 共线,且满足
共线,且满足 的向量
的向量 __________________
__________________
例1、已知 、
、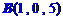 ,求:
,求:
(1)线段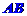 的中点坐标和长度;
的中点坐标和长度;
(2)到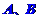 两点距离相等的点 的
两点距离相等的点 的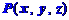 坐标
坐标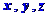 满足的条件。
满足的条件。
练:写出与点 距离等于4的点
距离等于4的点 的坐标
的坐标 满足的关系式。
满足的关系式。
例2、若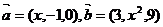 的夹角为钝角,求实数
的夹角为钝角,求实数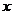 的取值范围。
的取值范围。
例3、在正方体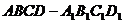 中,
中, 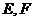 分别为
分别为 的中点.
的中点.
(1)求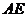 与
与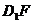 所成的角;
所成的角;
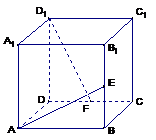 (2)证明:
(2)证明: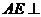 面
面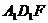
④、(链接)射影
定义:
提问: 方向上的投影:_____________
方向上的投影:_____________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com