
4、等差数列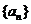 中,
中,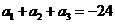 ,
,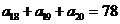 ,则此数列前20项和等于( )
,则此数列前20项和等于( )
A.160 B.180 C.200 D.220
3、已知数列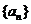 是公差为2的等差数列,且
是公差为2的等差数列,且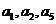 成等比数列,则
成等比数列,则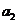 为( )
为( )
A.-2 B.-3 C.2 D.3
2、已知数列{an}满足: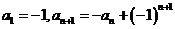 , nÎN*, 则
, nÎN*, 则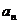 =( )
=( )
A.n B -n C.±n D.(-1)nn
-n C.±n D.(-1)nn
1、已知等差数列{an}的前n项和为Sn,若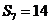 ,则
,则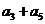 的值为 ( )
的值为 ( )
A.2 B.4 C.7 D.8
18. (1)第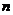 天销售的件数为
天销售的件数为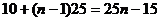
则4月30日的销售件数为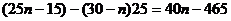
则: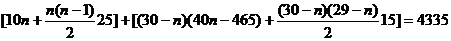
解得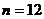 ,即4月12日的销售量最大,其最大值为25×12-15=285(件)
,即4月12日的销售量最大,其最大值为25×12-15=285(件)
(2)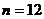 时,
时,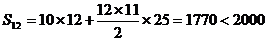 ,即未流行
,即未流行
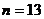 时,
时,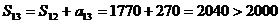
即从4月13日起,社会开始流行.
当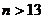 时,
时,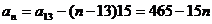 ,令
,令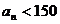 ,解得
,解得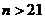
即从4月22日起,社会上流行消失,故流行的时间只有9天.
17.解:(1)由已知,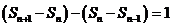 (
(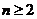 ,
,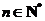 ),
),
即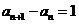 (
(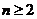 ,
,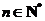 ),且
),且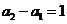 .
.
∴数列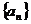 是以
是以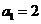 为首项,公差为1的等差数列.
为首项,公差为1的等差数列.
∴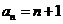 .
.
(2)∵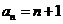 ,∴
,∴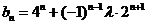 ,要使
,要使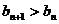 恒成立,
恒成立,
∴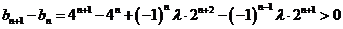 恒成立,
恒成立,
∴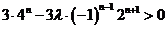 恒成立,
恒成立,
∴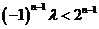 恒成立.(ⅰ)当
恒成立.(ⅰ)当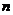 为奇数时,即
为奇数时,即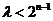 恒成立,
恒成立,
当且仅当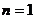 时,
时,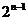 有最小值为1,
有最小值为1,
∴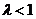 .(ⅱ)当
.(ⅱ)当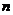 为偶数时,即
为偶数时,即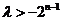 恒成立,
恒成立,
当且仅当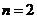 时,
时,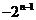 有最大值
有最大值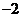 ,
,
∴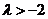 .即
.即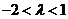 ,又
,又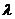 为非零整数,则
为非零整数,则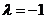 .
.
综上所述,存在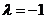 ,使得对任意
,使得对任意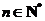 ,都有
,都有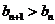 .
.
16.解:(Ⅰ)设等差数列{an}首项为a1,公差为d,由题意,得
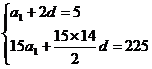 解得
解得 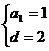 ∴an=2n-1
∴an=2n-1
(Ⅱ)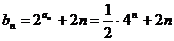 ,
,
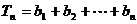
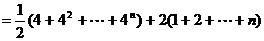
=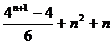
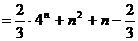
15.11
14.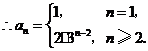
13.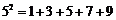 15
15
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com