
18. 已知向量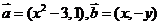 ,(其中实数
,(其中实数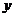 和
和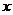 不同时为零),当
不同时为零),当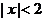 时,有
时,有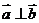 ,当
,当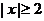 时,
时,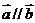 .
.
(1) 求函数式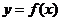 ;
;
(2)求函数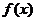 的单调递减区间;
的单调递减区间;
(3)若对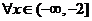
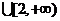 ,都有
,都有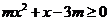 ,求实数
,求实数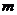 的取值范围.
的取值范围.
平面向量6答案
D B D A A D C
A B B 11,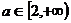
12, 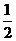 13,
13,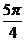 14,
14,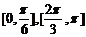 15,
15,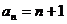
16, [解](1)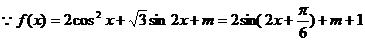 ,
,
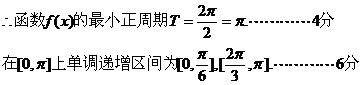
(2)当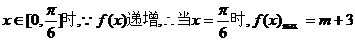 ,
,
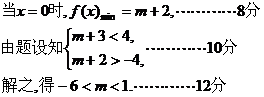
17,[解](Ⅰ)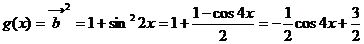
∴函数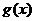 的最小周期
的最小周期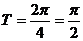
(Ⅱ)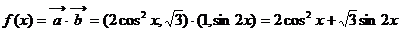
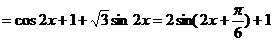
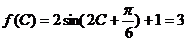
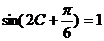
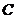 是三角形内角
是三角形内角
∴ , ∴
, ∴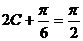 即:
即: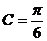
∴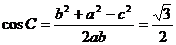 即:
即: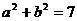
将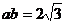 可得:
可得: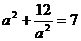 解之得:
解之得: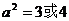 ∴
∴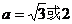
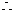
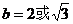 ,
, 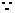
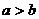 , ∴
, ∴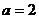
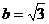 。
。
18,[解](1)当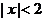 时,由
时,由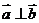 得
得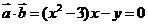 ,
,
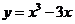 ;(
;(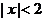 且
且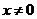 ),当
),当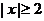 时,由
时,由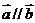 .得
.得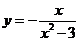 --
--
∴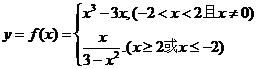
(2)当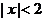 且
且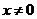 时,由
时,由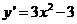 <0,解得
<0,解得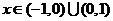 ,
,
当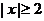 时,
时,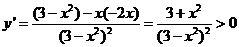
∴函数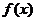 的单调减区间为(-1,0)和(0,1)
的单调减区间为(-1,0)和(0,1)
(3)对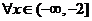
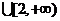 ,都有
,都有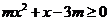 即
即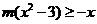 ,也就是
,也就是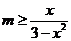 对
对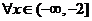
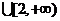 恒成立,
恒成立,
由(2)知当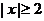 时,
时,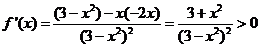
∴函数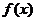 在
在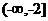 和
和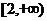 都单调递增
都单调递增
又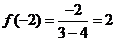 ,
,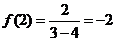
当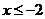 时
时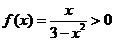 ,∴当
,∴当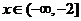 时,
时,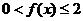
同文可得,当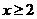 时,有
时,有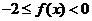 ,
,
综上所述得,对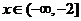
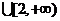 ,
, 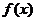 取得最大值2;
取得最大值2;
∴实数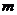 的取值范围为
的取值范围为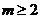 .
.
17.已知向量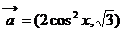 ,
, ,函数
,函数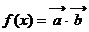 ,
,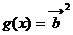 .
.
(Ⅰ)求函数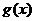 的最小正周期;
的最小正周期;
(Ⅱ)在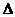
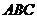 中,
中,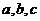 分别是角
分别是角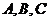 的对边,且
的对边,且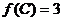 ,
,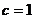 ,
,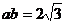 ,且
,且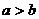 ,求
,求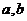 的值.
的值.
16.设函数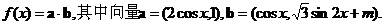
(1)求函数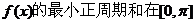 上的单调递增区间;
上的单调递增区间;
(2)当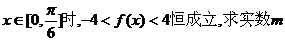 的取值范围。
的取值范围。
15.设向量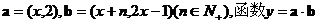 在[0,1]上的最大值与最小值的和an=
。
在[0,1]上的最大值与最小值的和an=
。
14.设函数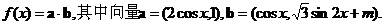
函数在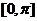 上的单调递增区间是
。
上的单调递增区间是
。
13.  已知A、B、C的坐标分别为A(3,0),B(0,3),C(
已知A、B、C的坐标分别为A(3,0),B(0,3),C(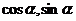 ),
),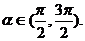
 若
若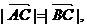 角
角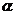 的值
.
的值
. 
12.已知ΔAOB中,点P在直线AB上,且满足: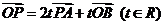 ,
,
则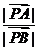 =
。
=
。
11、如果不等式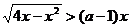 的解集为A,且
的解集为A,且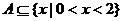 ,那么实数a的取值范围是
。
,那么实数a的取值范围是
。
10.设平面上有四个互异的点A、B、C、D,已知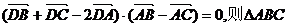 是(
) ( )
是(
) ( )
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等边三角形
9.已知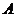 、
、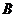 是抛物线
是抛物线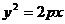 (
(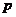 >0)上异于原点
>0)上异于原点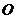 的两点,则“
的两点,则“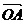 ·
·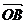 =0”是“直线
=0”是“直线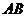 恒过定点(
恒过定点(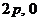 )”的( )
)”的( )
A.充分非必要条件 B.充要条件
C.必要非充分条件 D.非充分非必要条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com