
3.
已知函数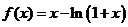 ,数列
,数列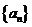 满足
满足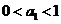 ,
,
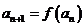 ; 数列
; 数列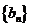 满足
满足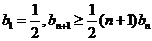 ,
, 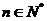 .求证:
.求证:
(Ⅰ)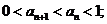
(Ⅱ)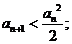
(Ⅲ)若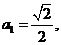 则当n≥2时,
则当n≥2时,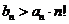 .
.
分析:第(1)问是和自然数有关的命题,可考虑用数学归纳法证明;第(2)问可利用函数的单调性;第(3)问进行放缩。
解:(Ⅰ)先用数学归纳法证明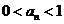 ,
,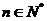 .
.
(1)当n=1时,由已知得结论成立;
(2)假设当n=k时,结论成立,即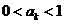 .则当n=k+1时,
.则当n=k+1时,
因为0<x<1时,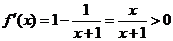 ,所以f(x)在(0,1)上是增函数.
,所以f(x)在(0,1)上是增函数.
又f(x)在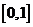 上连续,所以f(0)<f(
上连续,所以f(0)<f(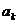 )<f(1),即0<
)<f(1),即0<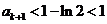 .
.
故当n=k+1时,结论也成立. 即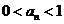 对于一切正整数都成立.
对于一切正整数都成立.
又由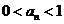 , 得
, 得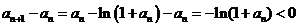 ,从而
,从而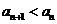 .
.
综上可知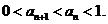
(Ⅱ)构造函数g(x)=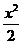 -f(x)=
-f(x)=
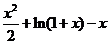 ,
0<x<1,
,
0<x<1,
由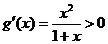 ,知g(x)在(0,1)上增函数.
,知g(x)在(0,1)上增函数.
又g(x)在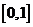 上连续,所以g(x)>g(0)=0.
上连续,所以g(x)>g(0)=0.
因为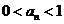 ,所以
,所以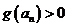 ,即
,即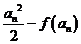 >0,从而
>0,从而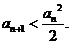
(Ⅲ) 因为 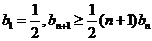 ,所以
,所以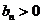 ,
,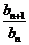
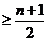 ,
,
所以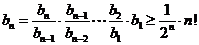 ----① ,
----① ,
由(Ⅱ)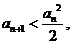 知:
知: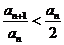 ,
,
所以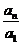 =
=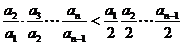 ,
,
因为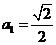 , n≥2,
, n≥2, 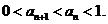
所以
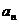
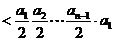 <
<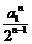 <
<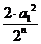 =
=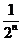 ----② .
----② .
由①② 两式可知: 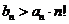 .
.
点评:本题是数列、超越函数、导数的学归纳法的知识交汇题,属于难题,复习时应引起注意。
2.
已知数列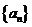 满足
满足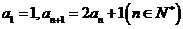
(Ⅰ)求数列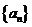 的通项公式;
的通项公式;
(Ⅱ)若数列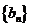 满足
满足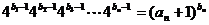 ,证明:
,证明: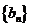 是等差数列;
是等差数列;
(Ⅲ)证明: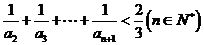
分析:本例(1)通过把递推关系式转化成等比型的数列;第(2)关键在于找出连续三项间的关系;第(3)问关键在如何放缩。
解:(1)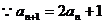 ,
,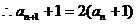
故数列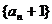 是首项为2,公比为2的等比数列。
是首项为2,公比为2的等比数列。
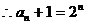 ,
,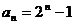
(2)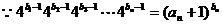 ,
,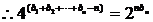
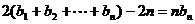 ①
①
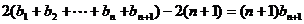 ②
②
②-①得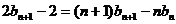 ,即
,即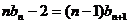 ③
③
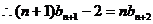 ④
④
④-③得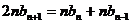 ,即
,即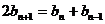
所以数列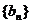 是等差数列
是等差数列
(3)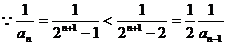
设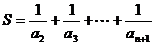 ,
,
则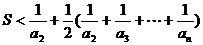
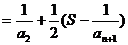
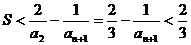
点评:数列中的不等式要用放缩来解决难度就较大了,而且不容易把握,对于这样的题要多探索,多角度的思考问题。
1.
已知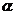 为锐角,且
为锐角,且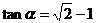 ,
,
函数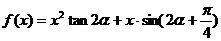 ,数列{an}的首项
,数列{an}的首项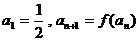 .
.
⑴ 求函数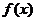 的表达式;
的表达式;
⑵ 求证: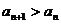 ;
;
⑶
求证: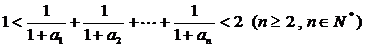
分析:本题是借助函数给出递推关系,第(2)问的不等式利用了函数的性质,第(3)问是转化成可以裂项的形式,这是证明数列中的不等式的另一种出路。
解:⑴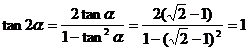 又∵
又∵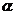 为锐角
为锐角
∴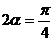 ∴
∴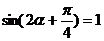
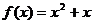
⑵ 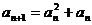 ∵
∵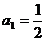 ∴
∴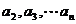 都大于0
都大于0
∴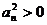 ∴
∴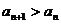
⑶ 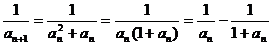
∴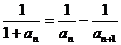
∴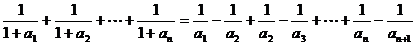
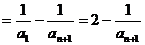
∵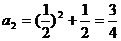 ,
, 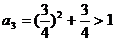 ,
,
又∵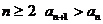
∴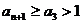 ∴
∴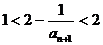
∴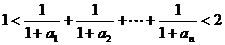
点评:把复杂的问题转化成清晰的问题是数学中的重要思想,本题中的第(3)问不等式的证明更具有一般性。
18。解:(1)依题意得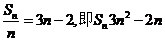
当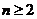 时
时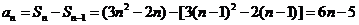 …①
…①
当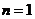 时,
时,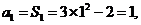 适合①式,所以,
适合①式,所以,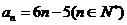 …5分
…5分
(2)由(1)得知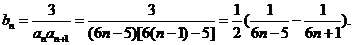
故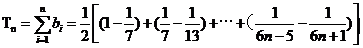
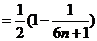 …9分
…9分
因此,使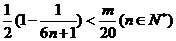 成立的
成立的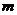 ,必须且仅须满足
,必须且仅须满足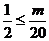 ,
,
即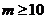 , 所以满足要求的最小正整数
, 所以满足要求的最小正整数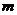 为10。
为10。
16。 解:(1)由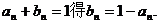 依题意
依题意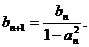
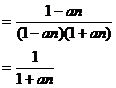
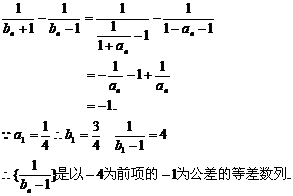
(2)由(1)知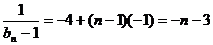
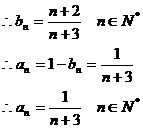
(3)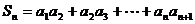
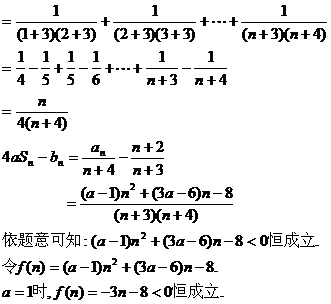
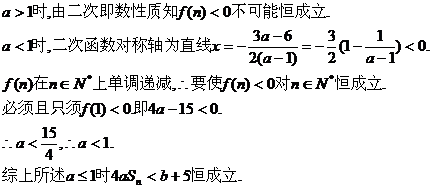
17 解(Ⅰ)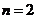 时,
时,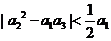 ,由已知
,由已知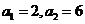 ,得
,得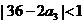 ,
,
因为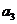 为正整数,所以
为正整数,所以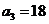 ,同理
,同理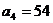
(Ⅱ)由(Ⅰ)可猜想: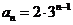 。
。
证明:①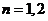 时,命题成立;
时,命题成立;
②假设当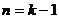 与
与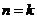 时成立,即
时成立,即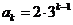 ,
,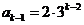 。
。
于是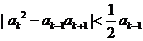 ,整理得:
,整理得: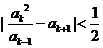 ,
,
由归纳假设得: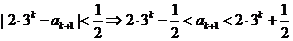 ,
,
因为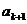 为正整数,所以
为正整数,所以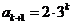 ,即当
,即当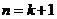 时命题仍成立。
时命题仍成立。
综上:由知①②知对于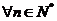 ,有
,有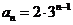 成立.
成立.
(Ⅲ)证明:由 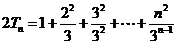 ③
③
得 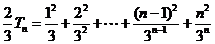 ④
④
③式减④式得 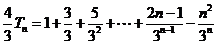 ⑤
⑤
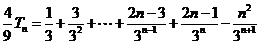 ⑥
⑥
⑤式减⑥式得
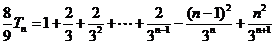
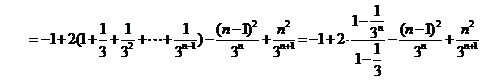
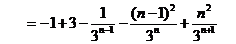
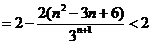
则 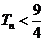 .
.
14。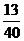 15.
15.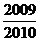
11。 1232 12。100. 5000; 13。2236
18、设数列{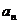 }的前n项和为
}的前n项和为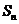 ,点
,点
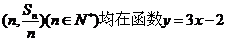 的图象上。
的图象上。
(1)求数列{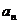 }的通项公式;
}的通项公式;
(2)设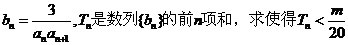 对所有
对所有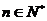 都成立的最小正整数m.
都成立的最小正整数m.
数列8答案
B D D B C A CA A C
17、设正整数数列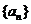 满足:
满足: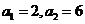 ,当
,当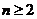 时,有
时,有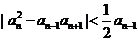 .
.
(I) 求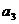 、
、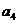 的值;
的值;
(Ⅱ)求数列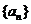 的通项;
的通项;
(Ⅲ) 记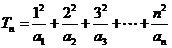 ,证明,对任意
,证明,对任意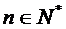 ,
,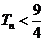 .
.
16、已知数列{an}、{bn}满足: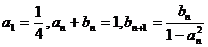 。
。
(1)求证:数列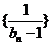 是等差数列;
是等差数列;
(2)求数列{an}的通项an;
(3)设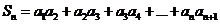 ,若
,若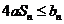 对于nÎN*恒成立,试求实数a的取值范围。
对于nÎN*恒成立,试求实数a的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com