
4.函数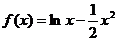 的图象大致是
的图象大致是
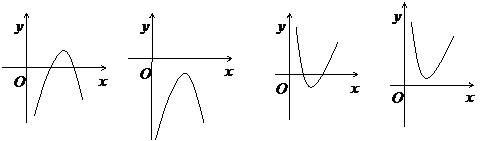
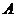 .
. 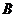 .
.  .
.  .
.
3.函数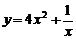 的单调递增区间是
的单调递增区间是
A.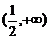 B.
B. 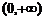 C.
C.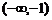 D.
D.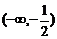
2.已知物体的运动方程为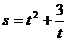 (t是时间,s是位移),则物体在时刻t=2时的速度为
(t是时间,s是位移),则物体在时刻t=2时的速度为
A.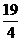 B.
B.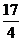 C.
C.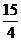 D.
D.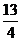
1.已知函数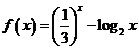 ,若实数
,若实数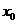 是方程
是方程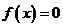 的解,且
的解,且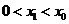 ,则
,则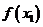 的值为
的值为
A.恒为正值 B.等于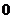 C.恒为负值 D.不大于
C.恒为负值 D.不大于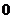
16. 解:(1)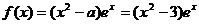
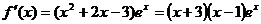
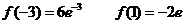
(2)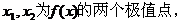
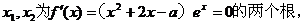
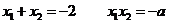
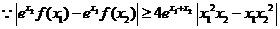
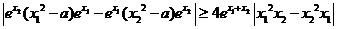
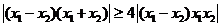
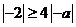 ,
, 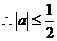
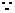 3
3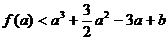 恒成立
恒成立
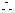 3
3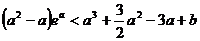 恒成立
恒成立
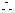
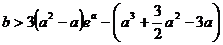 恒成立
恒成立
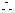
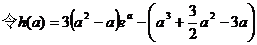
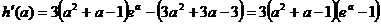
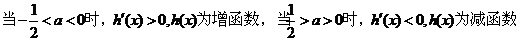
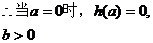
2.解:(1)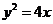
(2)设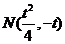 (t>0),则
(t>0),则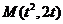 ,F(1,0)。
,F(1,0)。
因为M、F、N共线,则有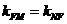 ,
,
所以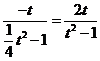 ,解得
,解得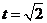 ,
,
所以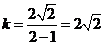 ,
,
因而,直线MN的方程是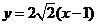 。
。
(3)“逆向问题”一:
①已知抛物线C: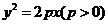 的焦点为F,过点F的直线交抛物线C于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过定点
的焦点为F,过点F的直线交抛物线C于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过定点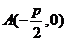 。
。
证明:设过F的直线为y=k(x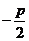 ),
),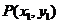 ,
,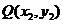 ,则
,则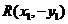
由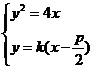 得
得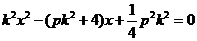 ,所以
,所以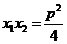 ,
,
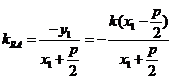 ,
,
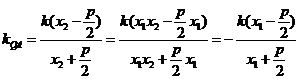 =
=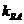 ,
,
所以直线RQ必过焦点A。
②过点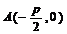 的直线交抛物线C于P、Q两点,FP与抛物线交于另一点R,则RQ垂直于x轴。
的直线交抛物线C于P、Q两点,FP与抛物线交于另一点R,则RQ垂直于x轴。
③已知抛物线C: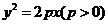 ,过点B(m,0 )(m>0)的直线交抛物线C于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过定点A(-m,0)。
,过点B(m,0 )(m>0)的直线交抛物线C于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过定点A(-m,0)。
“逆向问题”二:已知椭圆C: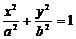 的焦点为F1(-c,0),F2(c,0),过F2的直线交椭圆C于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过定点
的焦点为F1(-c,0),F2(c,0),过F2的直线交椭圆C于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过定点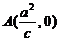 。
。
“逆向问题”三:已知双曲线C: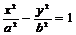 的焦点为F1(-c,0),F2(c,0),过F2的直线交双曲线C于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过定点
的焦点为F1(-c,0),F2(c,0),过F2的直线交双曲线C于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过定点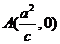 。
。
1. 解析:本例(1)通过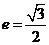 ,
,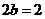 ,及
,及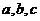 之间的关系可得椭圆的方程;(2)从方程入手,通过直线方程与椭圆方程组成方程组并结合韦达定理;(3)要注意特殊与一般的关系,分直线的斜率存在与不存在讨论。
之间的关系可得椭圆的方程;(2)从方程入手,通过直线方程与椭圆方程组成方程组并结合韦达定理;(3)要注意特殊与一般的关系,分直线的斜率存在与不存在讨论。
答案:(1)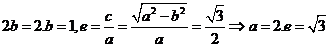
椭圆的方程为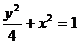
(2)设AB的方程为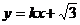 由
由
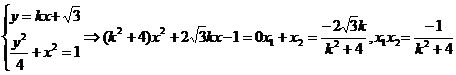 由已知
由已知
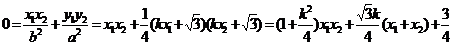
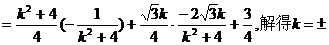 2
2
(3)当A为顶点时,B必为顶点.S△AOB=1
当A,B不为顶点时,设AB的方程为y=kx+b

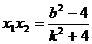
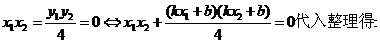
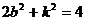
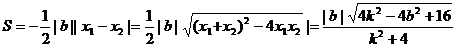
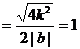
所以三角形的面积为定值.
点评:本题考查了直线与椭圆的基本概念和性质,二次方程的根与系数的关系、解析几何的基本思想方法以及运用综合知识解决问题的能力。
2.
已知抛物线C: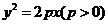 上任意一点到焦点F的距离比到y轴的距离大1。
上任意一点到焦点F的距离比到y轴的距离大1。
(1)求抛物线C的方程;
(2)若过焦点F的直线交抛物线于M、N两点,M在第一象限,且|MF|=2|NF|,求直线MN的方程;
(3)求出一个数学问题的正确结论后,将其作为条件之一,提出与原来问题有关的新问题,我们把它称为原来问题的一个“逆向”问题.
例如,原来问题是“若正四棱锥底面边长为4,侧棱长为3,求该正四棱锥的体积”.求出体积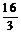 后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为
后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为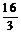 ,求侧棱长”;也可以是“若正四棱锥的体积为
,求侧棱长”;也可以是“若正四棱锥的体积为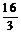 ,求所有侧面面积之和的最小值”.
,求所有侧面面积之和的最小值”.
现有正确命题:过点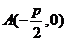 的直线交抛物线C:
的直线交抛物线C: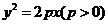 于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过焦点F。
于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过焦点F。
试给出上述命题的“逆向”问题,并解答你所给出的“逆向”问题。
1.
设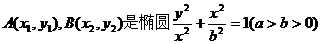 上的两点,
上的两点,
满足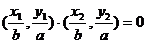 ,椭圆的离心率
,椭圆的离心率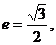 短轴长为2,0为坐标原点.
短轴长为2,0为坐标原点.
(1)求椭圆的方程;
(2)若直线AB过椭圆的焦点F(0,c),(c为半焦距),求直线AB的斜率k的值;
(3)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
17、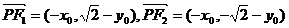 解:(1)由题可得
解:(1)由题可得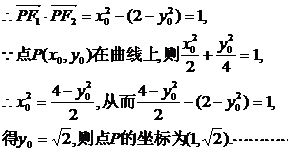
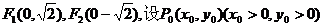
(2)由题意知,两直线PA、PB的斜率必存在,
设PB的斜率为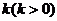 ,
,
则BP的直线方程为: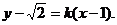

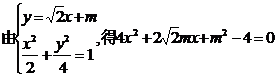
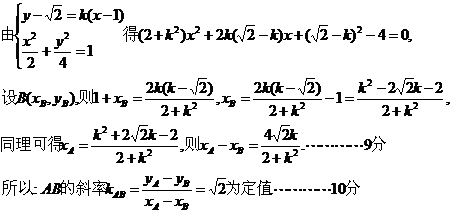 (3)设AB的直线方程:
(3)设AB的直线方程: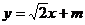
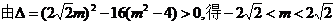 P到AB的距离
P到AB的距离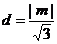 ,
,



 w
w
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com