解⑴当≥时，，，总成等差数列。

⑵若数列满足，求数列的前项和

⑴求数列的通项公式；

已知数列中，，前项和为，对于任意≥时，，，总成等差数列。

22. 荆州市2008届高中毕业班质量检测（Ⅱ）

  （3）由（2），得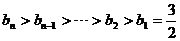

   ∴  即   ∴

   令，得(n+1)x₂－nx₁=1

  （2）由（1）知，对于（0，+）上的凹函数y=xⁿ⁺¹，有y’=(n+1)xⁿ，根据定理，得，整理，得，

  ∵{a_n}是正项数列，    ∴

  ∴数列{a_n}是以1为首项，1为公差的等差数列，从而a_n=n，

    ∴a_n =n  (n∈N*)