
结合上表可知猜想正确,即当n=3时f(n)取到最小值为f(3)= .………4分
.………4分
(Ⅱ)同解法一.
(Ⅲ)同解法一,得an=3n.………………………………………………………10分
由ai?aj=3i?3j=3i+j (1≤i≤j≤n),列表如下:
因为k≥5,所以2k2-(k+1)2=k2-2k-1=(k-1)2-2>0.
所以2k+1>(k+1)2.即当n=k+1时,不等式也成立.
根据(i)和(ii)所述,对于所有n≥5,n∈N *,n2<2 n都成立.
解法二:(Ⅰ)由f(n)=  ,计算得:
,计算得:
据此猜想n=3时,f(n)取到最小值.………………………………………2分
以下用数学归纳法证明n≥5时,n2<2 n成立.
(i)当n=5时,52<2 5,不等式成立.
(ii)假设n=k(k≥5)时不等式成立,即k2>2 k
那么2k+1=2 k ?2>k2 ?2 ,
=  ……………………………………………14分
……………………………………………14分
= 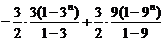
=  +
+ 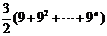
= 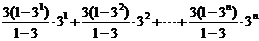
记数列{3 n}的所有可能的乘积 (1≤i≤j≤n)的和为S,则
(1≤i≤j≤n)的和为S,则
S=a1?a1+(a1+a2) ?a2+…+(a1+a2+…+an) ?an………………………………11分
= 3?31+(3+32) ?32+…+(3+32+…+3n) ?3n…………………………………12分
(Ⅲ)因为g(x)=2x,所以g(an+1)=
 ,又g(an+1)=
,又g(an+1)=
 =
=  ,
,
所以an+1=3an.又a1=3, 所以数列{an}是首项a1=3,公比为3的等比数列,
所以an=3?3 n-1=3 n. ………………………………………………………10分
综上,a>1时,原不等式的解集是(a+1,2a];a=1时,原不等式的解集是 ;
;
a<l时,原不等式的解集是(a+1,2].………………………………………9分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com