
7.已知三角形的顶点是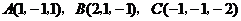 ,则这个三角形的面积等
,则这个三角形的面积等
于 .
答案: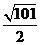
6.在棱长为1的正方体 中,
中, 分别是
分别是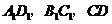 的中点,则
的中点,则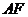 与
与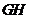 所成的角的余弦为( )
所成的角的余弦为( )
A.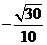 B.
B.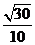 C.
C.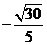 D.
D.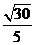
答案:B
5.在棱长为2的正方体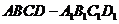 中,
中,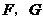 分别是
分别是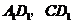 的中点,则
的中点,则 与平面
与平面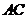 所成的角的余弦为( )
所成的角的余弦为( )
A.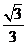 B.
B.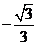 C.
C.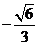 D.
D.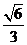
答案:D
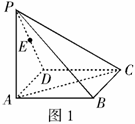
4.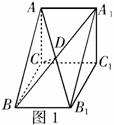 如图1,直三棱柱
如图1,直三棱柱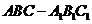 中,
中,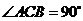 ,
,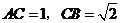 ,侧棱
,侧棱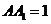 ,侧面
,侧面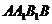 的两条对角线交点为
的两条对角线交点为 ,则面
,则面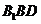 与面
与面 所成二面角的余弦值等于( )
所成二面角的余弦值等于( )
A.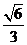 B.
B.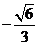 C.
C.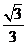 D.
D.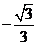
答案:D
3.已知点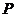 是平行四边形
是平行四边形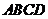 所在平面外一点,如果
所在平面外一点,如果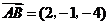 ,
,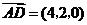 ,
,
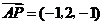 .对于结论:
.对于结论:
①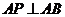 ;②
;②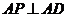 ;
;
③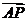 是平面
是平面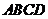 的法向量;
的法向量;
④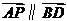 .
.
其中正确的个数是( )
A.1 B.2 C.3 D.4
答案:C
2.长方体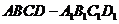 中,
中,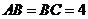 ,
,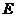 为
为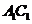 与
与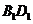 的交点,
的交点, 为
为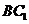 与
与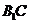 的交点,又
的交点,又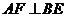 ,则长方体的高
,则长方体的高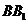 等于( )
等于( )
A.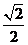 B.
B.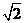 C.
C.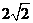 D.
D.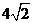
答案:C
1.已知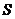 是边长为1的正三角形
是边长为1的正三角形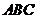 所在平面外一点,且
所在平面外一点,且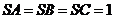 ,
,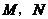 分别是
分别是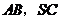 的中点,则异面直线
的中点,则异面直线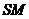 与
与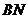 所成角的余弦值为( )
所成角的余弦值为( )
A.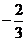 B.
B. C.
C.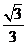 D.
D.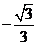
答案:B
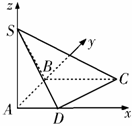
15.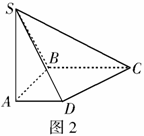 如图2,底面是直角梯形的四棱锥
如图2,底面是直角梯形的四棱锥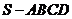 ,
,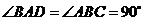 ,
,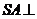 底面
底面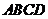 ,
,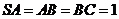 ,
, ,求面
,求面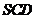 与面
与面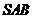 所成的二面角的余弦值.
所成的二面角的余弦值.
解:如图所示建立空间直角坐标系,
则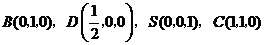 ,
,
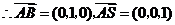 ,
,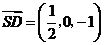 ,
,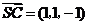 .
.
设平面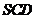 与平面
与平面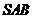 的法向量分别为
的法向量分别为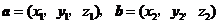 ,
,
 则由
则由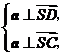 得
得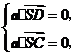
即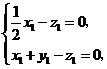
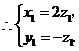
又由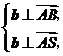 得
得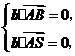 即
即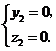
不妨令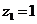 ,
,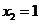 ,
,
则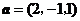 ,
,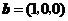 ,
,
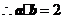 ,
,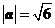 ,
,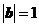 ,
,
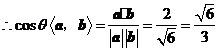 .
.
故面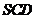 与面
与面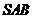 所成的二面角的余弦值为
所成的二面角的余弦值为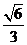 .
.

高中苏教选修(2-1)3.2空间向量的应用测试题
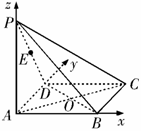
14.如图1,在四棱锥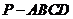 中,底面
中,底面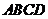 为矩形,侧棱
为矩形,侧棱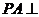 底面
底面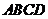 ,
,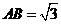 ,
,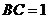 ,
,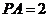 ,
,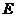 为
为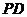 的中点.
的中点.
(1)求直线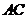 与
与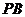 所成角的余弦值;
所成角的余弦值;
(2)在侧面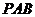 内找一点
内找一点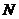 ,使
,使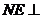 面
面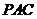 ,并求出
,并求出 点到直线
点到直线 和
和 的距离.
的距离.
解:(1)建立如图所示的空间直角坐标系,
 则
则 的坐标为
的坐标为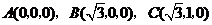 ,
,
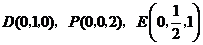 ,
,
从而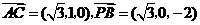 .
.
设 与
与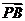 的夹角为
的夹角为 ,
,
则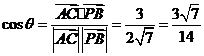 ,
,
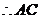 与
与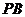 所成角的余弦值为
所成角的余弦值为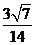 ;
;
(2)由于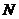 点在侧面
点在侧面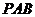 内,故可设
内,故可设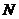 点坐标为
点坐标为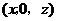 ,
,
则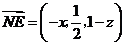 ,
,
由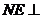 面
面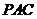 ,可得
,可得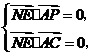
即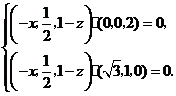
化简,得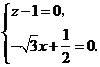
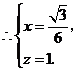
即 点的坐标为
点的坐标为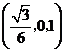 ,从而
,从而 点到
点到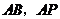 的距离分别为
的距离分别为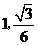 .
.
13.在棱长为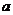 的正方体
的正方体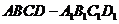 中,求异面直线
中,求异面直线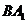 与
与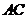 所成的角.
所成的角.
解: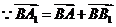 ,
,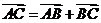 ,
,
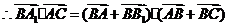
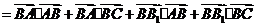 ,
,
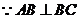 ,
, ,
,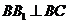 ,
,
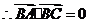 ,
,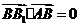 ,
,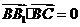 ,
,
又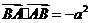 ,
,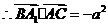 ,
,
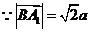 ,
,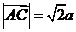 ,
,
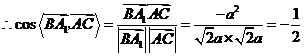 .
.
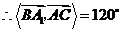 ,即异面直线
,即异面直线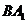 与
与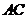 所成的角为
所成的角为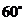 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com