
1、建立平面向量的坐标,基础是平面向量的基本定理及正交分解,对所给向量应会根据条件X轴和y轴进行分解求出其坐标。
10、已知 判断
判断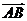 与
与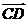 是否共线?
是否共线?
[名师小结、感悟反思]
9、证明下列各组点共线:
(1)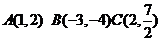 (2)
(2)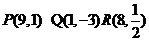
8、判断下列向量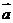 与
与 是否共线
是否共线
①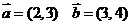 ②
②
7、已知A(-1,7)B(1,1)C(2,3)D(6,19)则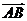 与
与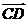 的关系为( )
的关系为( )
A.不共线 B.共线 C.相交 D.以上均不对
[举一反三、能力拓展]
6、下列各组向量相互平行的是( )
A.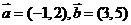
B.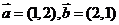
C.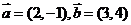
D.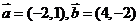
5、已知: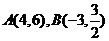 与
与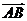 平行的向量的坐标可以是( )
平行的向量的坐标可以是( )
①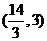 ②
②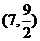 ③
③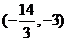 ④
④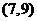
A.①② B.①②③ C.②③④ D.①②③④
4、已知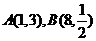 ,且A、B、C三点共线,则C点的坐标是( )
,且A、B、C三点共线,则C点的坐标是( )
A.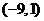 B.
B.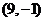 C.
C.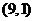 D.
D.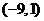
3、已知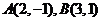 与
与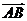 平行且方向相反的向量
平行且方向相反的向量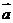 的是( )
的是( )
A.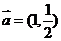 B.
B.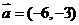 C.
C.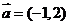 D.
D.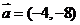
2、已知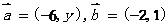 且
且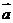 与
与 共线,则x=( )
共线,则x=( )
A.-6 B.6 C.3 D.-3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com