
∴线段AB的中点坐标为(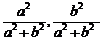 ).
).
解:(1)设A、B两点的坐标分别为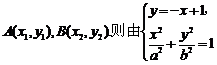 得
得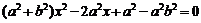 , 根据韦达定理,得
, 根据韦达定理,得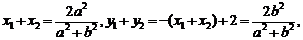
(Ⅱ)若椭圆的右焦点关于直线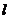 的对称点的在圆
的对称点的在圆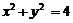 上,求此椭圆的方程.
上,求此椭圆的方程.
76、(江苏省前黄高级中学2008届高三调研)已知直线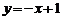 与椭圆
与椭圆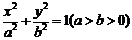 相交于A、B两点,且线段AB的中点在直线
相交于A、B两点,且线段AB的中点在直线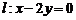 上.
上.
(Ⅰ)求此椭圆的离心率;
如果直线AB与⊙P相切,则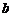 ?
?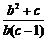 =-1. ………………………………………12分
=-1. ………………………………………12分
解出c=0或2,与0<c<1矛盾,………………………………………………………14分
所以直线AB与⊙P不能相切. …………………………………………………………15分
评讲建议:
此题主要考查直线与直线、直线与圆以及椭圆的相关知识,要求学生理解三角形外接圆圆心是三边中垂线的交点,从而大胆求出交点坐标,构造关于椭圆中a,b,c的齐次等式得离心率的范围.第二小题亦可以用平几的知识:圆的切割线定理,假设直线AB与⊙P相切,则有AB2=AF×AC,易由椭圆中a,b,c的关系推出矛盾.
由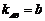 ,
,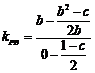 =
=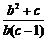 . ………………………………………………10分
. ………………………………………………10分
又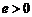 ,∴
,∴
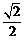 . …………………………………………………………………8分
. …………………………………………………………………8分
(Ⅱ)直线AB与⊙P不能相切.…………………………………………………………………9分
从而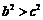 即有
即有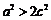 ,∴
,∴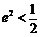 .……………………………………………………7分
.……………………………………………………7分
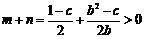 ,即
,即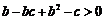 ,即(1+b)(b-c)>0,
,即(1+b)(b-c)>0,
∴ b>c. ……………………………………………………………………………………6分
联立方程组,解出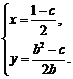 ……………………………………………………………4分
……………………………………………………………4分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com