2.(2009临沂一模)设函数f(x)=x²-mlnx,h(x)=x²-x+a.

(I)　　　　　　　　　 当a=0时，f(x)≥h(x)在(1,+∞)上恒成立，求实数m的取值范围;

(II)　　　　　　　　　 当m=2时，若函数k(x)=f(x)-h(x)在［1,3］上恰有两个不同零点，求实数 a的取值范围;

(III)　　　　　　　　　 是否存在实数m，使函数f(x)和函数h(x)在公共定义域上具有相同的单调性？若存在，求出m的值，若不存在，说明理由。

解：(1)由a=0,f(x)≥h(x)可得-mlnx≥-x　即

记，则f(x)≥h(x)在(1,+∞)上恒成立等价于.

求得

当时;;当时，

故在x=e处取得极小值，也是最小值，

即，故.

(2)函数k(x)=f(x)-h(x)在［1,3］上恰有两个不同的零点等价于方程x-2lnx=a，在［1,3］上恰有两个相异实根。

令g(x)=x-2lnx,则

当时，,当时，

g(x)在[1,2]上是单调递减函数，在上是单调递增函数。

故 又g(1)=1,g(3)=3-2ln3

∵g(1)>g(3),∴只需g(2)<a≤g(3),

故a的取值范围是(2-2ln2,3-2ln3)

(3)存在m=，使得函数f(x)和函数h(x)在公共定义域上具有相同的单调性

,函数f(x)的定义域为(0,+∞)。

若，则，函数f(x)在(0,+∞)上单调递增，不合题意;

若,由可得2x²-m>0，解得x>或x<-(舍去)

故时，函数的单调递增区间为(,+∞)

单调递减区间为(0, )而h(x)在(0,+∞)上的单调递减区间是(0,)，单调递增区间是(，+∞)

故只需=，解之得m=即当m=时，函数f(x)和函数h(x)在其公共定义域上具有相同的单调性。

2007-2008年联考题

1.(2009聊城一模)已知函数在区间[－1，1]上最大值为1，最小值为－2。

　 (1)求的解析式；

　 (2)若函数在区间[－2，2]上为减函数，求实数m的取值范围。

解：(1)

　 (2)

由，

知　　　　　　　　　　　　　　　　

，　 即　　　

6.(2009上海卢湾区4月模考)(2009上海卢湾区4月模考)设的反函数为，若函数的图像过点，且， 则　　　　 ．

答案

5.(2009上海十校联考)已知函数的值域是，则实数的取值范围是________________．

答案

4.(2009上海普陀区)已知函数，是的反函数，若的图像过点，则　　　　　 .

答案 2

3.(2009闵行三中模拟)若函数的值域是，则函数的值域是　　　

答案

2.(2009冠龙高级中学3月月考)已知函数，若，则实数的取值范围是　 　。

答案

1.(2009青岛一模)定义：区间的长度为.已知函数的定义域为，值域为，则区间的长度的最大值与最小值的差为_________.

答案 1

9.(2009枣庄一模)设函数　　　 (　　 )

　　　 A．3　　　　　　　　　　　　 B．4　　　　　　　　　　　　 C．7　　　　　　　　　　　　 D．9

答案 C

8.(2009枣庄一模)已知则关于右图中函数图象的表述正确的是　 (　　 )

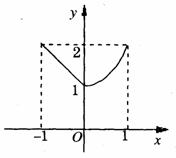　　　 A．是的图象　　　　　　　　　　　　　　

　　　 B．是的图象

　　　 C．是的图象　　　　　　　　

　　　 D．以上说法都不对

答案 D