22、(本题满分15分)已知函数　 且导数.

　(I)试用含有的式子表示，并求单调区间;

　(II)对于函数图象上的不同两点，如果在函数图象上存在点(其中)使得点处的切线，则称存在“伴侣切线”.特别地，当时，又称存在“中值伴侣切线”.试问：在函数上是否存在两点、使得它存在“中值伴侣切线”，若存在，求出、的坐标，若不存在，说明理由.

2009学年第一学期期末五校联考

21、(本题满分15分)已知椭圆的离心率为，点是椭圆上一定点，若斜率为的直线与椭圆交于不同的两点、.

(I)求椭圆方程；

(II)求面积的最大值.

20、(本题满分14分)一盒中装有分别标记着1，2，3，4数字的4个小球，每次从袋中取出

一只球，设每只小球被取出的可能性相同.

(I)若每次取出的球不放回盒中，现连续取三次球，求恰好第三次取出的球的标号为最大数字的球的概率；

(II)若每次取出的球放回盒中，然后再取出一只球，现连续取三次球，这三次取出的球中标号最大数字为，求的概率分布列与期望.

19、(本题满分14分)已知菱形的边长为2，对角线与交于点，且，为的中点.将此菱形沿对角线折成二面角.

(I)求证：面 面；

(II)若二面角为时，求直线 与面所成角的余弦值.

18、(本题满分14分)已知向量 ，，函数. 　

(Ⅰ)求的单调增区间；　

(II)若在中，角所对的边分别是，且满足：

，求的取值范围.

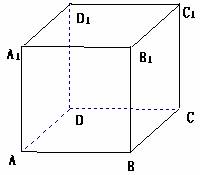
17、在边长为1的正方体中，P为正方　 体内一动点(包括表面)，若，且。则P点所有可能的位置所构成的几何体的体积是　　　　 .

16、有红、黄、蓝三种颜料可供选择去涂图中标号为1,2,3…9的9个小正方形(如图)，使得任意相邻(有公共边的)小正方形所涂颜色都不相同，且“3、5、7”号数字涂相同的颜色，则符合条件的所有涂法共有　　 种.

15、设实数满足不等式，若的最大值为1，则常数的取值范围是　　　　 .

14、直线与圆交于两点，为坐标原点，则　　 .

13、设f(x)=，则　　　　 .