
z=a+b取得最小值z=-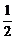 +2=
+2=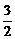 ,
,
当直线z=a+b经过交点P(-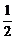 , 2)时,
, 2)时,

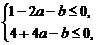 也即
也即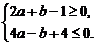 …………………9分
…………………9分
作出不等式组表示的平面区域如图:
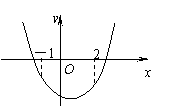 ∴ 当x=-1时, f (x)取极大值
∴ 当x=-1时, f (x)取极大值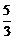 . …………………………6分
. …………………………6分
(2) ∵y=f (x)在区间[-1,2]上是单调减函数,
∴f ′(x)=x2+2ax-b≤0在区间[-1,2]上恒成立.
根据二次函数图象可知f ′(-1)≤0且f ′(2)≤0,即:
∴ f (x)=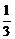 x3-x2-3x。
x3-x2-3x。
f ′(x)=x2-2x-3=(x+1)(x-3).
令f ′(x)=0,得x1=-1,x2=3,
由此可知:
x
(-∞,-1)
-1
(-1, 3)
3
(3, +∞)
f ’(x)
+
0
-
0
+
f (x)
ㄊ
f (x)极大5/3
ㄋ
f (x) 极小
ㄊ
∴ 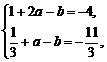 解得:
解得: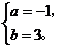 …………………………3分
…………………………3分
∴ 由题意可知:f ′(1)=-4且f (1)= -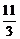 ,
,
(1)若y=f (x)图象上的点(1,-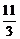 )处的切线斜率为-4,求y=f (x)的极大值;
)处的切线斜率为-4,求y=f (x)的极大值;
(2)若y=f (x)在区间[-1,2]上是单调减函数,求a + b的最小值.
【标准答案】
解:(1)∵f ′(x)=x2+2ax-b ,
11. 已知函数f (x)=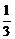 x3+ ax2-bx (a, b∈R) .
x3+ ax2-bx (a, b∈R) .
说明:本题在函数、导数、方程的交汇处命题,具有较强的预测性,而且设问的方式具有较大的开放性,情景新颖.解题的关键是:深刻理解函数“拐点”的定义和函数图像的对称中心的意义。其本质是:任何一个三次函数都有拐点;任何一个三次函数都有对称中心;且任何一个三次函数的拐点就是它的对称中心,即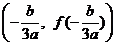 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com