
14 已知A、B、C是直线l上的三点,向量,,。满足:-[y+2f /(1)]+ln(x+1)=0.
(1)求函数y=f(x)的表达式;
(2)若x>0,证明:f(x)>;
(3)若不等式x2≤f(x2)+m2-2bm-3时,x∈[-1,1]及b∈[-1,1]都恒成立,
求实数m的取值范围.
【标准答案】
(1)∵-[y+2f /(1)]+ln(x+1)=0,∴=[y+2f /(1)]-ln(x+1)
由于A、B、C三点共线 即[y+2f /(1)]+[-ln(x+1)]=1
∴y=f(x)=ln(x+1)+1-2f /(1)
f /(x)=,得f /(1)=,故f(x)=ln(x+1) 4分
(2)令g(x)=f(x)―-,由g/(x)=-=
∵x>0,∴g/(x)>0,∴g(x)在(0,+∞)上是增函数
故g(x)>g(0)=0
即f(x)> 。 12分
(3)原不等式等价于x2-f(x2)≤m2-2bm-3。
令h(x)=x2-f(x2)=x2-ln(1+x2),由h/(x)=x-=
当x∈[-1,1]时,h(x)max=0,∴m2-2bm-3≥0
令Q(b)=m2-2bm-3,则
解得m≥3或m≤-3 。 12分
故-2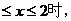 不等式f(x)
不等式f(x)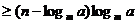 恒成立,
恒成立,
(3)由(2)知f(x)在[-2,2]上是减函数,则-2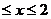 时,
时,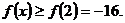
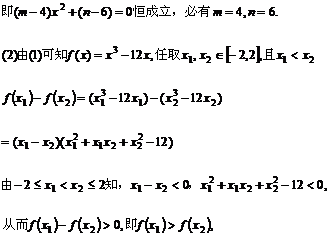
∴f(x)在[-2,2]上是减函数。
f(-x)=-f(x) 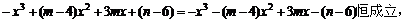
(3)当-2≤x≤2 时,不等式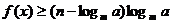 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
【标准答案】
(1)由于f(x)图象关于原点对称,则f(x)是奇函数,
13.已知 函数f(x)=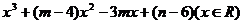 的图像关于原点对称,其中m,n为实常数。
的图像关于原点对称,其中m,n为实常数。
(1)求m , n的值;
(2)试用单调性的定义证明:f (x) 在区间[-2, 2] 上是单调函数;
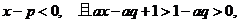 ∴
∴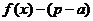 <0, ∴
<0, ∴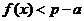 ,综上可知,
,综上可知,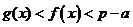 .
.
又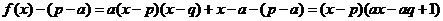 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com