
26.解析:设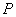 的坐标为
的坐标为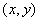 ,由题意有
,由题意有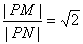 ,即
,即
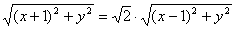 ,整理得
,整理得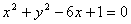
因为点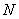 到
到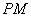 的距离为1,
的距离为1,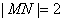
所以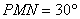 ,直线
,直线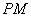 的斜率为
的斜率为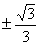
直线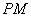 的方程为
的方程为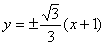
将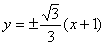 代入
代入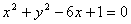 整理得
整理得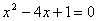
解得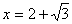 ,
,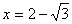
则点 坐标为
坐标为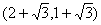 或
或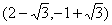
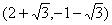 或
或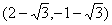
直线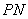 的方程为
的方程为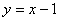 或
或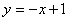 .
.
26.(02年全国卷文)(12分)
已知点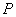 到两定点
到两定点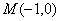 、
、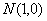 距离的比为
距离的比为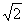 ,点
,点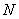 到直线
到直线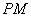 的距离为1,求直线
的距离为1,求直线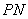 的方程。
的方程。
25.解析:(1) 抛物线y2=2px的准线为x=-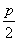 ,于是4+
,于是4+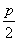 =5, ∴p=2.
=5, ∴p=2.
∴抛物线方程为y2=4x.
(2)∵点A是坐标是(4,4), 由题意得B(0,4),M(0,2),
又∵F(1,0), ∴kFA=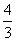 ;MN⊥FA, ∴kMN=-
;MN⊥FA, ∴kMN=-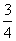 ,
,
则FA的方程为y=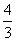 (x-1),MN的方程为y-2=-
(x-1),MN的方程为y-2=-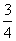 x,解方程组得x=
x,解方程组得x=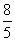 ,y=
,y=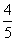 ,
,
∴N的坐标(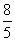 ,
,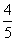 ).
).
(1) 由题意得, ,圆M.的圆心是点(0,2), 半径为2,
当m=4时, 直线AK的方程为x=4,此时,直线AK与圆M相离.
当m≠4时,
直线AK的方程为y=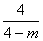 (x-m),即为4x-(4-m)y-
(x-m),即为4x-(4-m)y- 4m=0,
4m=0,
圆心M(0,2)到直线AK的距离d=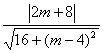 ,令d>2,解得m>1
,令d>2,解得m>1
∴当m>1时, AK与圆M相离;
当m=1时, AK与圆M相切;
当m<1时, AK与圆M相交.
25.(05年上海卷)(16分)
已知抛物线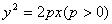 的焦点为F,A是抛物线上横坐标为4、且位于
的焦点为F,A是抛物线上横坐标为4、且位于 轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于
轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于 轴,垂足为B,OB的中点为M.
轴,垂足为B,OB的中点为M.
(1)求抛物线方程;
(2)过M作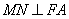 ,垂足为N,求点N的坐标;
,垂足为N,求点N的坐标;
(3)以M为圆心,MB为半径作圆M,当 是
是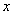 轴上一动点时,讨论直线AK与圆M的位置关系.
轴上一动点时,讨论直线AK与圆M的位置关系.
24.(05年山东卷理)(14分)
已知动圆过定点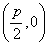 ,且与直线
,且与直线 相切,其中
相切,其中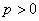 .
.
(I)求动圆圆心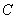 的轨迹的方程;
的轨迹的方程;
(II)设A、B是轨迹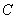 上异于原点
上异于原点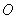 的两个不同点,直线
的两个不同点,直线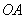 和
和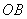 的倾斜角分别为
的倾斜角分别为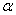 和
和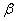 ,当
,当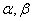 变化且
变化且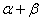 为定值
为定值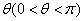 时,证明直线
时,证明直线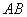 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
 24.
24.
解析:(I)如图,设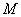 为动圆圆心,记
为动圆圆心,记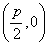 为
为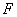 ,过点
,过点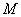 作直线
作直线 的垂线,垂足为
的垂线,垂足为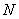 ,由题意知:
,由题意知: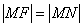 即动点
即动点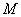 到定点
到定点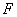 与定直线
与定直线 的距离相等
的距离相等
由抛物线的定义知,点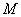 的轨迹为抛物线,其中
的轨迹为抛物线,其中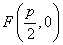 为焦点,
为焦点, 为准线
为准线
∴轨迹方程为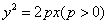 ;
;
(II)如图,设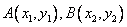 ,由题意得
,由题意得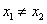 (否则
(否则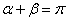 )且
)且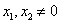
∴直线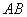 的斜率存在,设其方程为
的斜率存在,设其方程为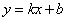
显然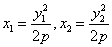

将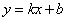 与
与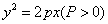 联立消去
联立消去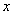 ,得
,得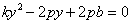
由韦达定理知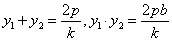 ①
①
(1)当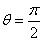 时,即
时,即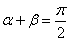 时,
时,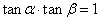
∴ ,
,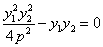
∴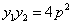
由①知: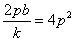
∴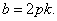
因此直线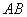 的方程可表示为
的方程可表示为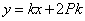 ,即
,即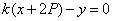
∴直线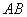 恒过定点
恒过定点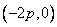
(2)当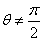 时,由
时,由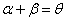 ,得
,得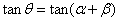 =
=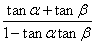 =
=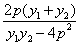
将①式代入上式整理化简可得: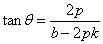 ,则
,则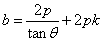 ,
,
此时,直线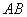 的方程可表示为
的方程可表示为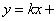
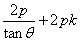 即
即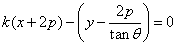
∴直线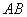 恒过定点
恒过定点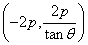
综上,由(1)(2)知,当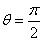 时,直线
时,直线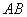 恒过定点
恒过定点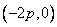 ,当
,当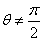 时直线
时直线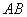 恒过定点
恒过定点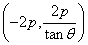 .
.
23.解析:(Ⅰ)设椭圆长半轴长及半焦距分别为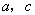 ,由已知得
,由已知得
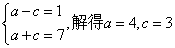 ,
,
所以椭圆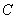 的标准方程为
的标准方程为
(Ⅱ)设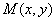 ,其中
,其中 。由已知
。由已知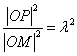 及点
及点 在椭圆
在椭圆 上可得
上可得
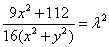 。
。
整理得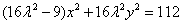 ,其中
,其中 。
。
(i)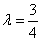 时。化简得
时。化简得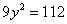
所以点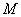 的轨迹方程为
的轨迹方程为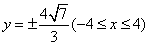 ,轨迹是两条平行于
,轨迹是两条平行于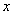 轴的线段。
轴的线段。
(ii)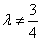 时,方程变形为
时,方程变形为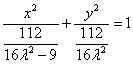 ,其中
,其中
当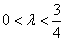 时,点
时,点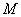 的轨迹为中心在原点、实轴在
的轨迹为中心在原点、实轴在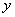 轴上的双曲线满足
轴上的双曲线满足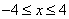 的部分。
的部分。
当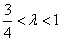 时,点
时,点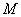 的轨迹为中心在原点、长轴在
的轨迹为中心在原点、长轴在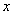 轴上的椭圆满足
轴上的椭圆满足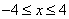 的部分;
的部分;
当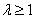 时,点
时,点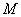 的轨迹为中心在原点、长轴在
的轨迹为中心在原点、长轴在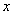 轴上的椭圆;
轴上的椭圆;
23.(2009宁夏海南卷理)(本小题满分12分)
已知椭圆C的中心为直角坐标系xOy的原点,焦点在s轴上,它的一个顶点到两个焦点的距离分别是7和1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若P为椭圆C上的动点,M为过P且垂直于x轴的直线上的点,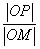 =λ,求点M的轨迹方程,并说明轨迹是什么曲线。
=λ,求点M的轨迹方程,并说明轨迹是什么曲线。
22.答案:
解析: 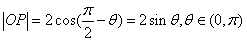
22.
 (07年上海卷理)已知圆的方程
(07年上海卷理)已知圆的方程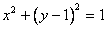 ,
, 为圆上任意一点(不包括原点)。直线
为圆上任意一点(不包括原点)。直线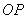 的倾斜角为
的倾斜角为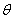 弧度,
弧度,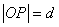 ,则
,则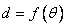 的图象大致为
的图象大致为
21.答案:
解析: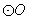 :圆心
:圆心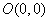 ,半径
,半径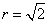 ;
;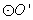 :圆心
:圆心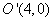 ,半径
,半径 .设
.设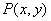 ,由切线长相等得
,由切线长相等得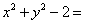
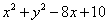 ,
, .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com