
88.(08山东济宁26题)(12分)
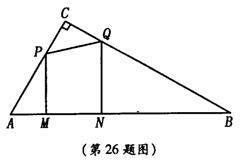
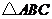 中,
中,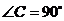 ,
,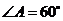 ,
,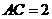 cm.长为1cm的线段
cm.长为1cm的线段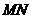 在
在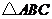 的边
的边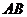 上沿
上沿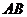 方向以1cm/s的速度向点
方向以1cm/s的速度向点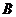 运动(运动前点
运动(运动前点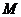 与点
与点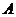 重合).过
重合).过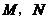 分别作
分别作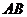 的垂线交直角边于
的垂线交直角边于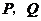 两点,线段
两点,线段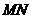 运动的时间为
运动的时间为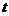 s.
s.
(1)若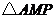 的面积为
的面积为 ,写出
,写出 与
与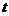 的函数关系式(写出自变量
的函数关系式(写出自变量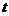 的取值范围);
的取值范围);
(2)线段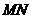 运动过程中,四边形
运动过程中,四边形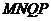 有可能成为矩形吗?若有可能,求出此时
有可能成为矩形吗?若有可能,求出此时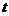 的值;若不可能,说明理由;
的值;若不可能,说明理由;
(3)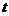 为何值时,以
为何值时,以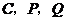 为顶点的三角形与
为顶点的三角形与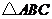 相似?
相似?
(08山东济宁26题解析)解:(1)当点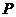 在
在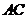 上时,
上时,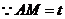 ,
,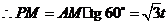 .
.
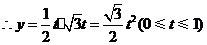 .········································································ 2分
.········································································ 2分
当点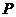 在
在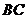 上时,
上时,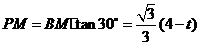 .
.
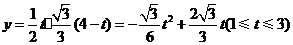 .·················································· 4分
.·················································· 4分
(2)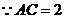 ,
,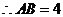 .
.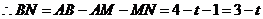 .
.
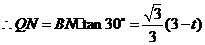 .········································································ 6分
.········································································ 6分
由条件知,若四边形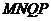 为矩形,需
为矩形,需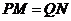 ,即
,即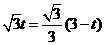 ,
,
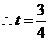 .
.
 当
当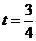 s时,四边形
s时,四边形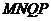 为矩形.································································· 8分
为矩形.································································· 8分
(3)由(2)知,当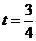 s时,四边形
s时,四边形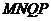 为矩形,此时
为矩形,此时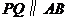 ,
,
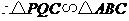 .··························································································· 9分
.··························································································· 9分
除此之外,当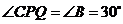 时,
时,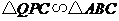 ,此时
,此时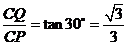 .
.
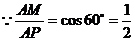 ,
,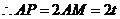 .
.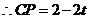 .····························· 10分
.····························· 10分
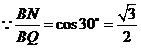 ,
,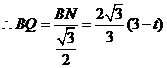 .
.
又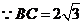 ,
,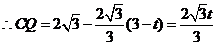 .········································ 11分
.········································ 11分
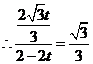 ,
,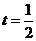 .
.
 当
当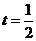 s或
s或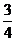 s时,以
s时,以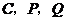 为顶点的三角形与
为顶点的三角形与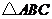 相似.··················· 12分
相似.··················· 12分
87.(08青海省卷28题)王亮同学善于改进学习方法,他发现对解题过程进行回顾反思,效果会更好.某一天他利用30分钟时间进行自主学习.假设他用于解题的时间 (单位:分钟)与学习收益量
(单位:分钟)与学习收益量 的关系如图甲所示,用于回顾反思的时间
的关系如图甲所示,用于回顾反思的时间 (单位:分钟)与学习收益量
(单位:分钟)与学习收益量 的关系如图乙所示(其中
的关系如图乙所示(其中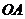 是抛物线的一部分,
是抛物线的一部分,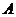 为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
(1)求王亮解题的学习收益量 与用于解题的时间
与用于解题的时间 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)求王亮回顾反思的学习收益量 与用于回顾反思的时间
与用于回顾反思的时间 之间的函数关系式;
之间的函数关系式;
(3)王亮如何分配解题和回顾反思的时间,才能使这30分钟的学习收益总量最大?
(学习收益总量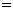 解题的学习收益量
解题的学习收益量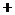 回顾反思的学习收益量)
回顾反思的学习收益量)
(08青海省卷28题解析)解:(1)设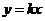 ,
,
把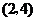 代入,得
代入,得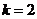 .
.
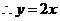 .······································································································ (1分)
.······································································································ (1分)
自变量 的取值范围是:
的取值范围是: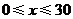 .···························································· (2分)
.···························································· (2分)
(2)当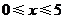 时,
时,
设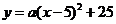 ,···················································································· (3分)
,···················································································· (3分)
把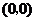 代入,得
代入,得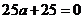 ,
,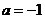 .
.
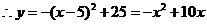 .································································· (5分)
.································································· (5分)
当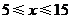 时,
时,
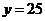 ············································································································· (6分)
············································································································· (6分)
即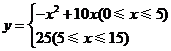 .
.
(3)设王亮用于回顾反思的时间为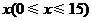 分钟,学习效益总量为
分钟,学习效益总量为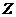 ,
,
则他用于解题的时间为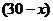 分钟.
分钟.
当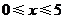 时,
时,
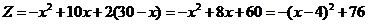 .························· (7分)
.························· (7分)
 当
当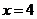 时,
时,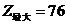 .············································································ (8分)
.············································································ (8分)
当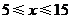 时,
时,
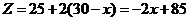 .····································································· (9分)
.····································································· (9分)
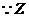 随
随 的增大而减小,
的增大而减小,
 当
当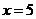 时,
时,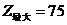 .
.
综合所述,当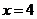 时,
时,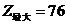 ,此时
,此时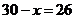 .································ (10分)
.································ (10分)
即王亮用于解题的时间为26分钟,用于回顾反思的时间为4分钟时,学习收益总量最大.
······················································································································· (11分)
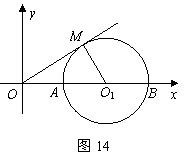
86.(08青海西宁28题)如图14,已知半径为1的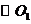 与
与 轴交于
轴交于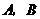 两点,
两点,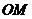 为
为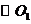 的切线,切点为
的切线,切点为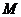 ,圆心
,圆心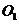 的坐标为
的坐标为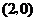 ,二次函数
,二次函数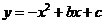 的图象经过
的图象经过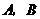 两点.
两点.
(1)求二次函数的解析式;
 (2)求切线
(2)求切线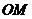 的函数解析式;
的函数解析式;
(3)线段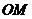 上是否存在一点
上是否存在一点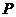 ,使得以
,使得以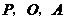 为顶点的三角形与
为顶点的三角形与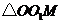 相似.若存在,请求出所有符合条件的点
相似.若存在,请求出所有符合条件的点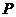 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(08青海西宁28题解析)解:(1)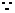 圆心
圆心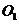 的坐标为
的坐标为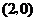 ,
,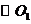 半径为1,
半径为1,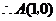 ,
,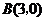 ……1分
……1分
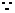 二次函数
二次函数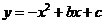 的图象经过点
的图象经过点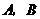 ,
,
 可得方程组
可得方程组 ················································································ 2分
················································································ 2分
解得: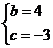
 二次函数解析式为
二次函数解析式为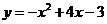 ············································· 3分
············································· 3分
(2)过点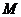 作
作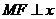 轴,垂足为
轴,垂足为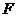 .······························································· 4分
.······························································· 4分
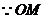 是
是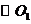 的切线,
的切线,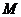 为切点,
为切点,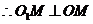 (圆的切线垂直于经过切点的半径).
(圆的切线垂直于经过切点的半径).
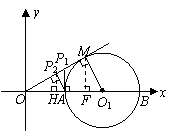 在
在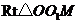 中,
中,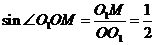
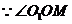 为锐角,
为锐角,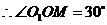 ···························· 5分
···························· 5分
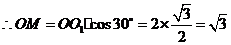 ,
,
在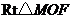 中,
中,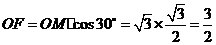 .
.
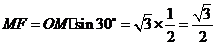 .
.
 点
点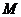 坐标为
坐标为 ························································································· 6分
························································································· 6分
设切线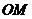 的函数解析式为
的函数解析式为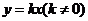 ,由题意可知
,由题意可知 ,
,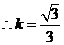 ······ 7分
······ 7分
 切线
切线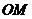 的函数解析式为
的函数解析式为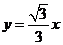 ···································································· 8分
···································································· 8分
(3)存在.············································································································ 9分
①过点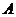 作
作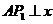 轴,与
轴,与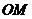 交于点
交于点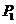 .可得
.可得 (两角对应相等两三角形相似)
(两角对应相等两三角形相似)
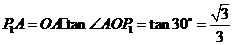 ,
,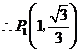 ············································ 10分
············································ 10分
②过点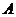 作
作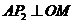 ,垂足为
,垂足为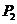 ,过
,过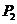 点作
点作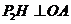 ,垂足为
,垂足为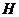 .
.
可得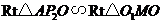 (两角对应相等两三角开相似)
(两角对应相等两三角开相似)
在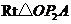 中,
中,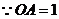 ,
,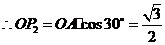 ,
,
在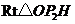 中,
中,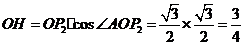 ,
,
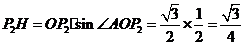 ,
,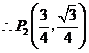 ······································· 11分
······································· 11分
 符合条件的
符合条件的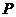 点坐标有
点坐标有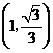 ,
,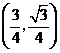 ······················································ 12分
······················································ 12分
85.(08内蒙古赤峰25题)(本题满分14分)
在平面直角坐标系中给定以下五个点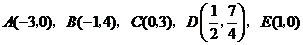 .
.
(1)请从五点中任选三点,求一条以平行于 轴的直线为对称轴的抛物线的解析式;
轴的直线为对称轴的抛物线的解析式;
(2)求该抛物线的顶点坐标和对称轴,并画出草图;
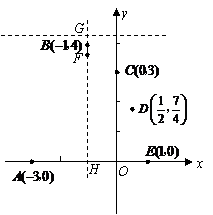 (3)已知点
(3)已知点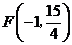 在抛物线的对称轴上,直线
在抛物线的对称轴上,直线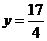 过点
过点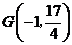 且垂直于对称轴.验证:以
且垂直于对称轴.验证:以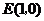 为圆心,
为圆心,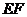 为半径的圆与直线
为半径的圆与直线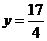 相切.请你进一步验证,以抛物线上的点
相切.请你进一步验证,以抛物线上的点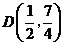 为圆心
为圆心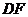 为半径的圆也与直线
为半径的圆也与直线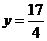 相切.由此你能猜想到怎样的结论.
相切.由此你能猜想到怎样的结论.
(08内蒙古赤峰25题解析)25.解:(1)设抛物线的解析式为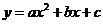 ,
,
且过点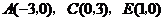 ,
,
由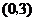 在
在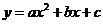 H .
H .
则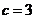 .········································································································ (2分)
.········································································································ (2分)
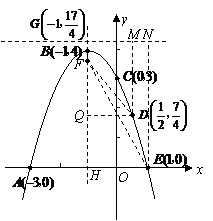 得方程组
得方程组 ,
,
解得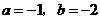 .
.
 抛物线的解析式为
抛物线的解析式为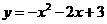 ················ (4分)
················ (4分)
(2)由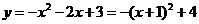 ············· (6分)
············· (6分)
得顶点坐标为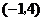 ,对称轴为
,对称轴为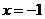 .·········· (8分)
.·········· (8分)
(3)①连结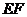 ,过点
,过点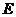 作直线
作直线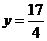 的垂线,垂足为
的垂线,垂足为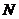 ,
,
则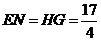 .
.
在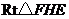 中,
中,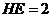 ,
,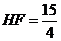 ,
,
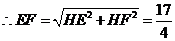 ,
,
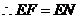 ,
,
 以
以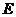 点为圆心,
点为圆心,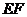 为半径的
为半径的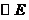 与直线
与直线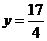 相切.····························· (10分)
相切.····························· (10分)
②连结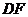 过点
过点 作直线
作直线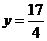 的垂线,垂足为
的垂线,垂足为 .过点
.过点 作
作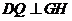 垂足为
垂足为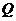 ,
,
则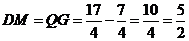 .
.
在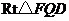 中,
中,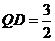 ,
, .
.
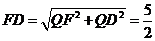 .
.
 以
以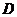 点为圆心
点为圆心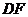 为半径的
为半径的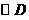 与直线
与直线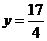 相切.································ (12分)
相切.································ (12分)
③以抛物线上任意一点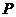 为圆心,以
为圆心,以 为半径的圆与直线
为半径的圆与直线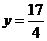 相切.····· (14分)
相切.····· (14分)
84.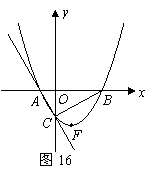 (08辽宁12市26题)(本题14分)26.如图16,在平面直角坐标系中,直线
(08辽宁12市26题)(本题14分)26.如图16,在平面直角坐标系中,直线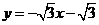 与
与 轴交于点
轴交于点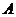 ,与
,与 轴交于点
轴交于点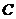 ,抛物线
,抛物线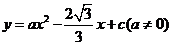 经过
经过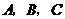 三点.
三点.
(1)求过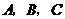 三点抛物线的解析式并求出顶点
三点抛物线的解析式并求出顶点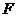 的坐标;
的坐标;
(2)在抛物线上是否存在点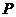 ,使
,使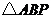 为直角三角形,若存在,直接写出
为直角三角形,若存在,直接写出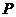 点坐标;若不存在,请说明理由;
点坐标;若不存在,请说明理由;
(3)试探究在直线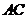 上是否存在一点
上是否存在一点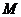 ,使得
,使得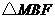 的周长最小,若存在,求出
的周长最小,若存在,求出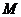 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
(08辽宁12市26题解析)
解:(1)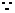 直线
直线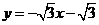 与
与 轴交于点
轴交于点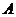 ,与
,与 轴交于点
轴交于点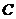 .
.
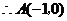 ,
,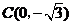 ························································································· 1分
························································································· 1分
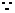 点
点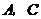 都在抛物线上,
都在抛物线上,
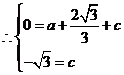
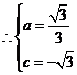
 抛物线的解析式为
抛物线的解析式为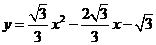 ························································ 3分
························································ 3分
 顶点
顶点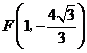 ······························································································· 4分
······························································································· 4分
(2)存在··············································································································· 5分
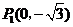 ············································································································· 7分
············································································································· 7分
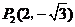 ············································································································ 9分
············································································································ 9分
(3)存在·············································································································· 10分
理由:
解法一:
延长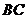 到点
到点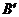 ,使
,使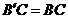 ,连接
,连接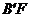 交直线
交直线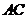 于点
于点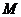 ,则点
,则点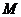 就是所求的点.
就是所求的点.
····················································································· 11分
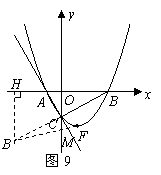 过点
过点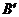 作
作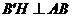 于点
于点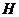 .
.
 点在抛物线
点在抛物线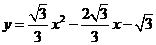 上,
上,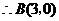
在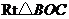 中,
中,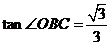 ,
,
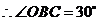 ,
,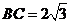 ,
,
在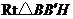 中,
中,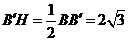 ,
,
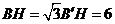 ,
,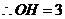 ,
,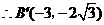 ··············································· 12分
··············································· 12分
设直线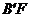 的解析式为
的解析式为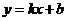
 解得
解得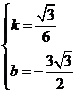
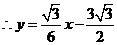 ································································································ 13分
································································································ 13分
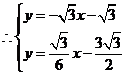 解得
解得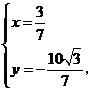
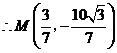
 在直线
在直线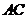 上存在点
上存在点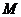 ,使得
,使得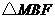 的周长最小,此时
的周长最小,此时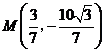 .··· 14分
.··· 14分
解法二:
 过点
过点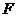 作
作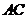 的垂线交
的垂线交 轴于点
轴于点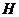 ,则点
,则点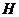 为点
为点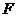 关于直线
关于直线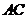 的对称点.连接
的对称点.连接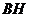 交
交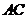 于点
于点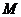 ,则点
,则点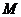 即为所求.················································································ 11分
即为所求.················································································ 11分
过点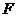 作
作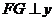 轴于点
轴于点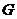 ,则
,则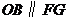 ,
,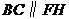 .
.
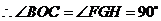 ,
,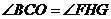
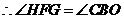
同方法一可求得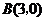 .
.
在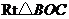 中,
中,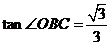 ,
,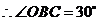 ,可求得
,可求得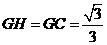 ,
,
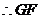 为线段
为线段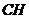 的垂直平分线,可证得
的垂直平分线,可证得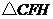 为等边三角形,
为等边三角形,
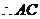 垂直平分
垂直平分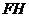 .
.
即点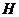 为点
为点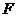 关于
关于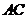 的对称点.
的对称点.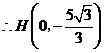 ············································· 12分
············································· 12分
设直线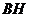 的解析式为
的解析式为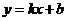 ,由题意得
,由题意得
 解得
解得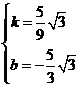
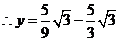 ································································································ 13分
································································································ 13分
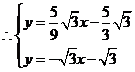 解得
解得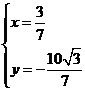
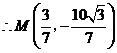
 在直线
在直线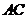 上存在点
上存在点 ,使得
,使得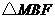 的周长最小,此时
的周长最小,此时 .··· 14分
.··· 14分
83. (08辽宁沈阳26题)(本题14分)26.如图所示,在平面直角坐标系中,矩形
(08辽宁沈阳26题)(本题14分)26.如图所示,在平面直角坐标系中,矩形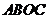 的边
的边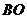 在
在 轴的负半轴上,边
轴的负半轴上,边 在
在 轴的正半轴上,且
轴的正半轴上,且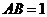 ,
,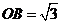 ,矩形
,矩形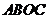 绕点
绕点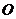 按顺时针方向旋转
按顺时针方向旋转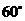 后得到矩形
后得到矩形 .点
.点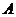 的对应点为点
的对应点为点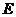 ,点
,点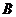 的对应点为点
的对应点为点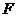 ,点
,点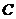 的对应点为点
的对应点为点 ,抛物线
,抛物线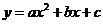 过点
过点 .
.
(1)判断点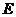 是否在
是否在 轴上,并说明理由;
轴上,并说明理由;
(2)求抛物线的函数表达式;
(3)在 轴的上方是否存在点
轴的上方是否存在点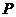 ,点
,点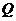 ,使以点
,使以点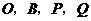 为顶点的平行四边形的面积是矩形
为顶点的平行四边形的面积是矩形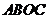 面积的2倍,且点
面积的2倍,且点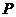 在抛物线上,若存在,请求出点
在抛物线上,若存在,请求出点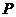 ,点
,点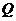 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(08辽宁沈阳26题解析)解:(1)点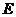 在
在 轴上················································· 1分
轴上················································· 1分
理由如下:
连接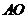 ,如图所示,在
,如图所示,在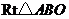 中,
中,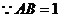 ,
,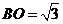 ,
,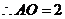
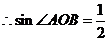 ,
,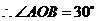
由题意可知: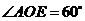
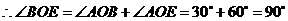
 点
点 在
在 轴上,
轴上, 点
点 在
在 轴上.········································································· 3分
轴上.········································································· 3分
(2)过点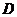 作
作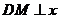 轴于点
轴于点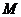
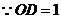 ,
,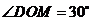
 在
在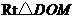 中,
中,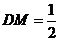 ,
,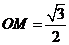
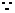 点
点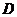 在第一象限,
在第一象限,
 点
点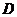 的坐标为
的坐标为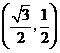 ·························································································· 5分
·························································································· 5分
由(1)知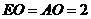 ,点
,点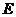 在
在 轴的正半轴上
轴的正半轴上
 点
点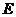 的坐标为
的坐标为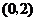
 点
点 的坐标为
的坐标为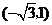 ···························································································· 6分
···························································································· 6分
 抛物线
抛物线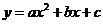 经过点
经过点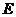 ,
,
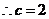
由题意,将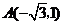 ,
, 代入
代入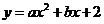 中得
中得
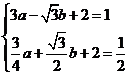 解得
解得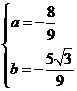
 所求抛物线表达式为:
所求抛物线表达式为: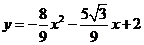 ······················································· 9分
······················································· 9分
(3)存在符合条件的点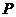 ,点
,点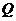 .········································································· 10分
.········································································· 10分
理由如下: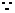 矩形
矩形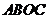 的面积
的面积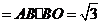
 以
以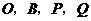 为顶点的平行四边形面积为
为顶点的平行四边形面积为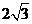 .
.
由题意可知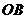 为此平行四边形一边,
为此平行四边形一边,
又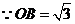
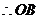 边上的高为2··································································································· 11分
边上的高为2··································································································· 11分
依题意设点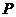 的坐标为
的坐标为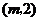
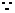 点
点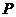 在抛物线
在抛物线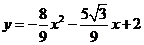 上
上
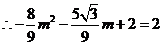
解得,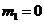 ,
,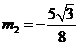
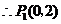 ,
,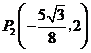
 以
以 为顶点的四边形是平行四边形,
为顶点的四边形是平行四边形,
 ,
,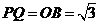 ,
,
 当点
当点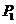 的坐标为
的坐标为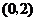 时,
时,
点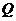 的坐标分别为
的坐标分别为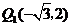 ,
,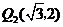 ;
;
当点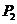 的坐标为
的坐标为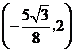 时,
时,
点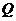 的坐标分别为
的坐标分别为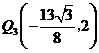 ,
,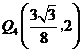 .··············································· 14分
.··············································· 14分
82.(08广东肇庆25题)(本小题满分10分)
已知点A(a,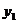 )、B(2a,y
)、B(2a,y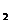 )、C(3a,y
)、C(3a,y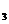 )都在抛物线
)都在抛物线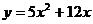 上.
上.
(1)求抛物线与x轴的交点坐标;
(2)当a=1时,求△ABC的面积;
(3)是否存在含有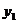 、y
、y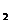 、y
、y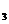 ,且与a无关的等式?如果存在,试给出一个,并加以证明;如果不存在,说明理由.
,且与a无关的等式?如果存在,试给出一个,并加以证明;如果不存在,说明理由.
(08广东肇庆25题解析)(本小题满分10分)
解:(1)由5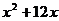 =0,·············································································· (1分)
=0,·············································································· (1分)
得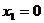 ,
,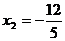 .·················································································· (2分)
.·················································································· (2分)
∴抛物线与x轴的交点坐标为(0,0)、( ,0).······································· (3分)
,0).······································· (3分)
(2)当a=1时,得A(1,17)、B(2,44)、C(3,81),······························ (4分)
分别过点A、B、C作x轴的垂线,垂足分别为D、E、F,则有
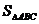 =S
=S -
- -
- ···················································· (5分)
···················································· (5分)
=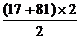 -
- -
-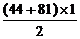 ···································· (6分)
···································· (6分)
=5(个单位面积)········································································ (7分)
(3)如: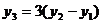 . ········································································· (8分)
. ········································································· (8分)
事实上,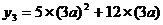 =45a2+36a.
=45a2+36a.
3(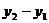 )=3[5×(2a)2+12×2a-(5a2+12a)] =45a2+36a.············ (9分)
)=3[5×(2a)2+12×2a-(5a2+12a)] =45a2+36a.············ (9分)
∴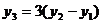 . ···················································································· (10分)
. ···················································································· (10分)
81.(08广东茂名25题)(本题满分10分)
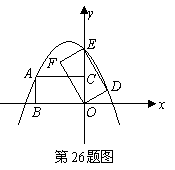
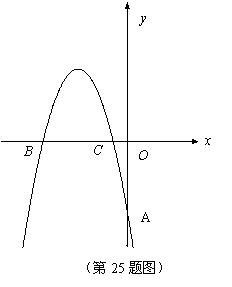 如图,在平面直角坐标系中,抛物线
如图,在平面直角坐标系中,抛物线 =-
=-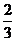

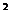 +
+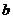
 +
+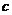 经过A(0,-4)、B(
经过A(0,-4)、B(
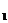 ,0)、 C(
,0)、 C(
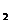 ,0)三点,且
,0)三点,且
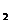 -
-
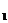 =5.
=5.
(1)求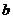 、
、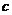 的值;(4分)
的值;(4分)
(2)在抛物线上求一点D,使得四边形BDCE是以BC为对 角线的菱形;(3分)
(3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线的菱形?若存在,求出点P的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.(3分)
解:
(08广东茂名25题解析)解:(1)解法一:
∵抛物线 =-
=-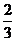

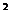 +
+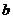
 +
+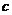 经过点A(0,-4),
经过点A(0,-4),
∴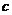 =-4 ……1分
=-4 ……1分
又由题意可知,
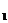 、
、
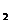 是方程-
是方程-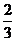

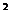 +
+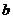
 +
+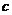 =0的两个根,
=0的两个根,
∴
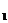 +
+
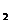 =
=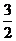
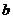 ,
,

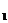

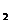 =-
=-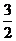
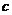 =6··································································· 2分
=6··································································· 2分
由已知得(
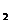 -
-
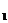 )
)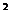 =25
=25
又(
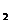 -
-
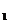 )
)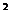 =(
=(
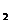 +
+
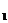 )
)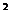 -4
-4
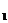

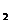 =
=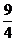
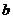
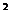 -24
-24
∴ 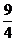
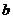
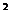 -24=25
-24=25
解得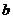 =±
=±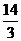 ··········································································································· 3分
··········································································································· 3分
当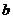 =
=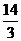 时,抛物线与
时,抛物线与 轴的交点在
轴的交点在 轴的正半轴上,不合题意,舍去.
轴的正半轴上,不合题意,舍去.
∴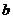 =-
=-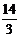 . ·········································································································· 4分
. ·········································································································· 4分
解法二:∵
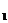 、
、
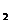 是方程-
是方程-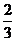

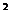 +
+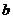
 +c=0的两个根,
+c=0的两个根,
即方程2
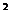 -3
-3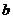
 +12=0的两个根.
+12=0的两个根.
∴ =
=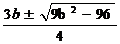 ,··········································································· 2分
,··········································································· 2分
∴
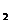 -
-
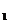 =
=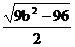 =5,
=5,
解得 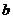 =±
=±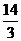 ······························································································· 3分
······························································································· 3分
(以下与解法一相同.)
(2)∵四边形BDCE是以BC为对角线的菱形,根据菱形的性质,点D必在抛物线的对称轴上, 5分
又∵ =-
=-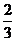

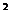 -
-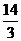
 -4=-
-4=-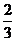 (
( +
+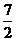 )
)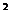 +
+ ································· 6分
································· 6分
∴抛物线的顶点(-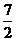 ,
, )即为所求的点D.······································· 7分
)即为所求的点D.······································· 7分
(3)∵四边形BPOH是以OB为对角线的菱形,点B的坐标为(-6,0),
根据菱形的性质,点P必是直线 =-3与
=-3与
抛物线 =-
=-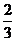

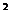 -
-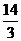
 -4的交点, ···························································· 8分
-4的交点, ···························································· 8分
∴当 =-3时,
=-3时, =-
=-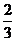 ×(-3)
×(-3)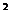 -
-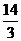 ×(-3)-4=4,
×(-3)-4=4,
∴在抛物线上存在一点P(-3,4),使得四边形BPOH为菱形. ·················· 9分
四边形BPOH不能成为正方形,因为如果四边形BPOH为正方形,点P的坐标只能是(-3,3),但这一点不在抛物线上.······································································································· 10分
76.(08天津市卷26题)(本小题10分)
已知抛物线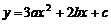 ,
,
(Ⅰ)若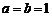 ,
,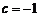 ,求该抛物线与
,求该抛物线与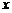 轴公共点的坐标;
轴公共点的坐标;
(Ⅱ)若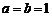 ,且当
,且当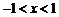 时,抛物线与
时,抛物线与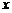 轴有且只有一个公共点,求
轴有且只有一个公共点,求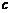 的取值范围;
的取值范围;
(Ⅲ)若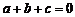 ,且
,且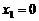 时,对应的
时,对应的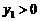 ;
;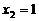 时,对应的
时,对应的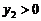 ,试判断当
,试判断当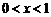 时,抛物线与
时,抛物线与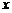 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
(08天津市卷26题解析)解(Ⅰ)当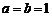 ,
,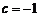 时,抛物线为
时,抛物线为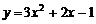 ,
,
方程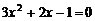 的两个根为
的两个根为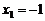 ,
,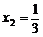 .
.
∴该抛物线与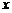 轴公共点的坐标是
轴公共点的坐标是 和
和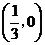 .
················································ 2分
.
················································ 2分
(Ⅱ)当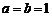 时,抛物线为
时,抛物线为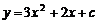 ,且与
,且与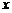 轴有公共点.
轴有公共点.
对于方程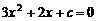 ,判别式
,判别式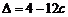 ≥0,有
≥0,有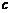 ≤
≤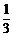 . ········································ 3分
. ········································ 3分
①当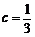 时,由方程
时,由方程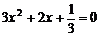 ,解得
,解得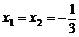 .
.
此时抛物线为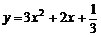 与
与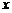 轴只有一个公共点
轴只有一个公共点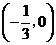 .·································
4分
.·································
4分
②当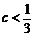 时,
时,
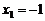 时,
时, ,
,
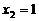 时,
时, .
.
由已知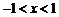 时,该抛物线与
时,该抛物线与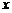 轴有且只有一个公共点,考虑其对称轴为
轴有且只有一个公共点,考虑其对称轴为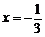 ,
,
应有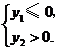 即
即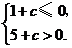
解得 .
.
综上,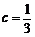 或
或 . ················································································ 6分
. ················································································ 6分
(Ⅲ)对于二次函数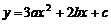 ,
,
由已知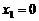 时,
时,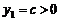 ;
;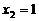 时,
时,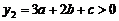 ,
,
又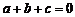 ,∴
,∴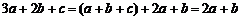 .
.
于是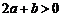 .而
.而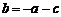 ,∴
,∴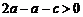 ,即
,即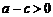 .
.
∴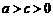 .
············································································································ 7分
.
············································································································ 7分
∵关于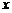 的一元二次方程
的一元二次方程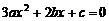 的判别式
的判别式
 ,
,
∴抛物线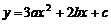 与
与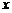 轴有两个公共点,顶点在
轴有两个公共点,顶点在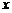 轴下方.····························· 8分
轴下方.····························· 8分
又该抛物线的对称轴 ,
,
 由
由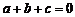 ,
,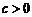 ,
,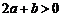 ,
,
得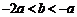 ,
,
∴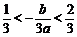 .
.
又由已知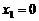 时,
时,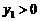 ;
;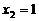 时,
时,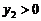 ,观察图象,
,观察图象,
可知在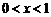 范围内,该抛物线与
范围内,该抛物线与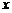 轴有两个公共点. ············································ 10分
轴有两个公共点. ············································ 10分
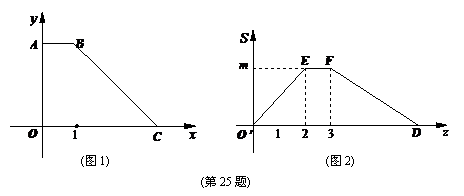
77(08湖北宜昌25题)如图1,已知四边形OABC中的三个顶点坐标为O(0,0),A(0,n),C(m,0).动点P从点O出发依次沿线段OA,AB,BC向点C移动,设移动路程为z,△OPC的面积S随着z的变化而变化的图象如图2所示.m,n是常数, m>1,n>0.
(1)请你确定n的值和点B的坐标;
 (2)当动点P是经过点O,C的抛物线y=ax
(2)当动点P是经过点O,C的抛物线y=ax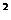 +bx+c的顶点,且在双曲线y=
+bx+c的顶点,且在双曲线y= 上时,求这时四边形OABC的面积.
上时,求这时四边形OABC的面积.
(08湖北宜昌25题解析)解:(1) 从图中可知,当P从O向A运动时,△POC的面积S=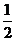 mz, z由0逐步增大到2,则S由0逐步增大到m,故OA=2,n=2 . (1分)
mz, z由0逐步增大到2,则S由0逐步增大到m,故OA=2,n=2 . (1分)
同理,AB=1,故点B的坐标是(1,2).(2分)
(2)解法一:
∵抛物线y=ax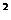 +bx+c经过点O(0,0),C(m ,0),∴c=0,b=-am,(3分)
+bx+c经过点O(0,0),C(m ,0),∴c=0,b=-am,(3分)
∴抛物线为y=ax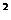 -amx,顶点坐标为(
-amx,顶点坐标为(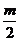 ,-am2).(4分)
,-am2).(4分)
 如图1,设经过点O,C,P的抛物线为l.
如图1,设经过点O,C,P的抛物线为l.
当P在OA上运动时,O,P都在y轴上,
这时P,O,C三点不可能同在一条抛物线上,
∴这时抛物线l不存在, 故不存在m的值..①
当点P与C重合时,双曲线y= 不可能经过P,
不可能经过P,
故也不存在m的值.②(5分)
(说明:①②任做对一处评1分,两处全对也只评一分)
当P在AB上运动时,即当0<x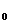 ≤1时,y
≤1时,y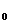 =2,
=2,
抛物线l的顶点为P(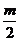 ,2).
,2).
∵P在双曲线y= 上,可得 m=
上,可得 m=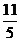 ,∵
,∵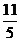 >2,与 x
>2,与 x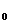 =
=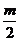 ≤1不合,舍去.(6分)③
≤1不合,舍去.(6分)③
容易求得直线BC的解析式是: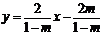 ,(7分)
,(7分)
当P在BC上运动,设P的坐标为 (x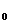 ,y
,y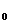 ),当P是顶点时 x
),当P是顶点时 x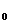 =
=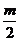 ,
,
故得y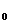 =
=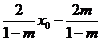 =
=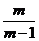 ,顶点P为(
,顶点P为(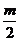 ,
,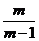 ),
),
∵1< x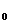 =
=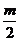 <m,∴m>2,又∵P在双曲线y=
<m,∴m>2,又∵P在双曲线y= 上,
上,
于是,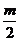 ×
×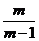 =
=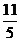 ,化简后得5m
,化简后得5m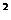 -22m+22=0,
-22m+22=0,
解得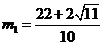 ,
, ,(8分)
,(8分)
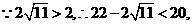
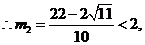
与题意2<x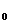 =
=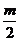 <m不合,舍去.④(9分)
<m不合,舍去.④(9分)
故由①②③④,满足条件的只有一个值: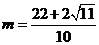 .
.
这时四边形OABC的面积= =
=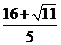 .(10分)
.(10分)
(2)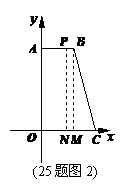 解法二:
解法二:
∵抛物线y=ax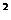 +bx+c经过点O(0,0),C(m ,0)
+bx+c经过点O(0,0),C(m ,0)
∴c=0,b=-am,(3分)
∴抛物线为y=ax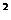 -amx,顶点坐标P为(,-am2). (4分)
-amx,顶点坐标P为(,-am2). (4分)
∵m>1,∴>0,且≠m,
∴P不在边OA上且不与C重合. (5分)
∵P在双曲线y=上,∴×(- am2)=即a=- .
.①当1<m≤2时,<≤1,如图2,分别过B,P作x轴的垂线,
M,N为垂足,此时点P在线段AB上,且纵坐标为2,
∴-am2=2,即a=-.
而a=- ,∴- =-,m=>2,而1<m≤2,不合题意,舍去.(6分)
②当m≥2时,>1,如图3,分别过B,P作x轴的垂线,M,N为垂足,ON>OM,
此时点P在线段CB上,易证Rt△BMC∽Rt△PNC,
∴BM∶PN=MC∶NC,即: 2∶PN=(m-1)∶,∴PN=(7分)
而P的纵坐标为- am2,∴=- am2,即a=
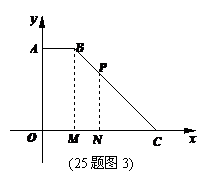 而a=-,∴- =
而a=-,∴- =
化简得:5m2-22m+22=0.解得:m= ,(8分)
但m≥2,所以m=舍去,(9分)
取m = .
由以上,这时四边形OABC的面积为:
(AB+OC) ×OA=(1+m) ×2=. (10分)
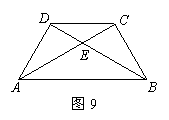
74.(08广东东莞22题)(本题满分9分)将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边
AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连结CD.
(1)填空:如图9,AC= ,BD= ;四边形ABCD是 梯形.
(2)请写出图9中所有的相似三角形(不含全等三角形).
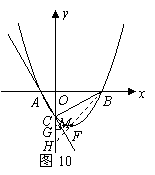
(3)如图10,若以AB所在直线为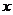 轴,过点A垂直于AB的直线为
轴,过点A垂直于AB的直线为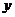 轴建立如图10的平面直角坐标系,保持ΔABD不动,将ΔABC向
轴建立如图10的平面直角坐标系,保持ΔABD不动,将ΔABC向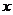 轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围.
轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围.

(08广东东莞22题解析)解:(1)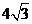 ,
,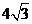 ,…………………………1分
,…………………………1分
等腰;…………………………2分
(2)共有9对相似三角形.(写对3-5对得1分,写对6-8对得2分,写对9对得3分)
①△DCE、△ABE与△ACD或△BDC两两相似,分别是:△DCE∽△ABE,△DCE∽△ACD,△DCE∽△BDC,△ABE∽△ACD,△ABE∽△BDC;(有5对)
②△ABD∽△EAD,△ABD∽△EBC;(有2对)
③△BAC∽△EAD,△BAC∽△EBC;(有2对)
所以,一共有9对相似三角形.…………………………………………5分
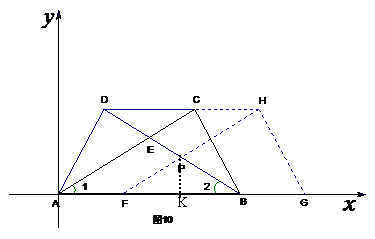
(3)由题意知,FP∥AE,
∴ ∠1=∠PFB,
又∵ ∠1=∠2=30°,
∴ ∠PFB=∠2=30°,
∴ FP=BP.…………………………6分
过点P作PK⊥FB于点K,则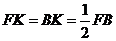 .
.
∵ AF=t,AB=8,
∴ FB=8-t,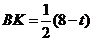 .
.
在Rt△BPK中,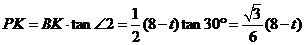 . ……………………7分
. ……………………7分
∴ △FBP的面积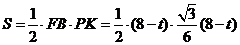 ,
,
∴ S与t之间的函数关系式为:
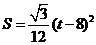 ,或
,或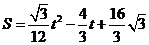 . …………………………………8分
. …………………………………8分
t的取值范围为: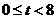 . …………………………………………………………9分
. …………………………………………………………9分
75(08甘肃兰州28题)(本题满分12分)如图19-1,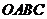 是一张放在平面直角坐标系中的矩形纸片,
是一张放在平面直角坐标系中的矩形纸片,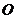 为原点,点
为原点,点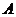 在
在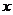 轴的正半轴上,点
轴的正半轴上,点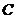 在
在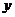 轴的正半轴上,
轴的正半轴上,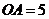 ,
,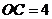 .
.
(1)在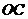 边上取一点
边上取一点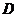 ,将纸片沿
,将纸片沿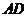 翻折,使点
翻折,使点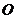 落在
落在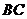 边上的点
边上的点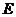 处,求
处,求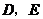 两点的坐标;
两点的坐标;
(2)如图19-2,若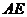 上有一动点
上有一动点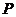 (不与
(不与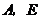 重合)自
重合)自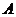 点沿
点沿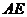 方向向
方向向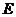 点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为
点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为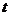 秒(
秒(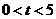 ),过
),过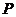 点作
点作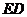 的平行线交
的平行线交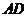 于点
于点 ,过点
,过点 作
作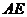 的平行线交
的平行线交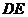 于点
于点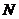 .求四边形
.求四边形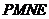 的面积
的面积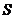 与时间
与时间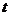 之间的函数关系式;当
之间的函数关系式;当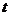 取何值时,
取何值时,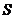 有最大值?最大值是多少?
有最大值?最大值是多少?
(3)在(2)的条件下,当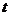 为何值时,以
为何值时,以 为顶点的三角形为等腰三角形,并求出相应的时刻点
为顶点的三角形为等腰三角形,并求出相应的时刻点 的坐标.
的坐标.
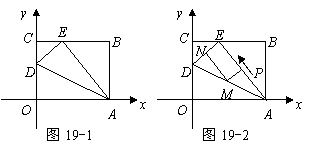
(08甘肃兰州28题解析)(本题满分12分)
解:(1)依题意可知,折痕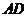 是四边形
是四边形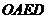 的对称轴,
的对称轴,
 在
在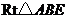 中,
中,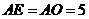 ,
,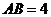 .
.
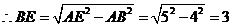 .
.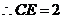 .
.
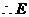 点坐标为(2,4).································································································ 2分
点坐标为(2,4).································································································ 2分
在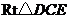 中,
中,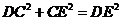 , 又
, 又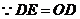 .
.
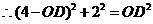 . 解得:
. 解得: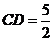 .
.
 点坐标为
点坐标为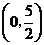 ···································································································· 3分
···································································································· 3分
(2)如图①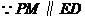 ,
,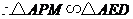 .
.
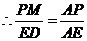 ,又知
,又知 ,
,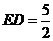 ,
,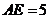
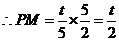 , 又
, 又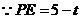 .
.
而显然四边形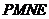 为矩形.
为矩形.
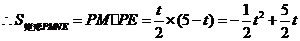 ·························································· 5分
·························································· 5分
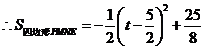 ,又
,又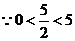
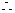 当
当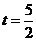 时,
时,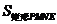 有最大值
有最大值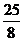 .········································································ 6分
.········································································ 6分
(3)(i)若以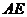 为等腰三角形的底,则
为等腰三角形的底,则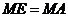 (如图①)
(如图①)
在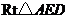 中,
中,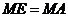 ,
,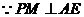 ,
,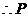 为
为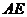 的中点,
的中点,
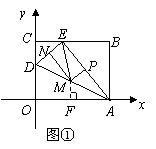
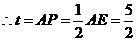 .
.
又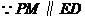 ,
,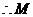 为
为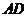 的中点.
的中点.
过点 作
作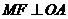 ,垂足为
,垂足为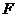 ,则
,则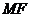 是
是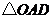 的中位线,
的中位线,
 ,
,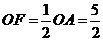 ,
,
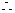 当
当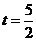 时,
时,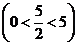 ,
,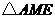 为等腰三角形.
为等腰三角形.
此时 点坐标为
点坐标为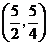 .··························································································· 8分
.··························································································· 8分
(ii)若以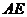 为等腰三角形的腰,则
为等腰三角形的腰,则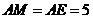 (如图②)
(如图②)
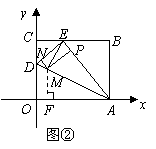 在
在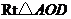 中,
中,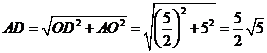 .
.
过点 作
作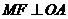 ,垂足为
,垂足为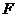 .
.
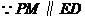 ,
,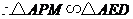 .
.
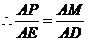 .
.
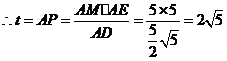 ,
,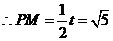 .
.
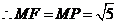 ,
,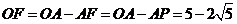 ,
,
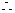 当
当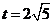 时,(
时,( ),此时
),此时 点坐标为
点坐标为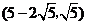 .·························· 11分
.·························· 11分
综合(i)(ii)可知,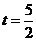 或
或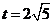 时,以
时,以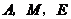 为顶点的三角形为等腰三角形,相应
为顶点的三角形为等腰三角形,相应 点的坐标为
点的坐标为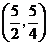 或
或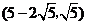 .·········································································································· 12分
.·········································································································· 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com