
14.(2008·江苏20)若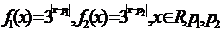 为常数,
为常数,
且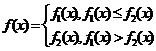
(I)求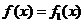 对所有的实数
对所有的实数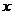 成立的充要条件(用
成立的充要条件(用 表示);
表示);
(II)设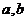 为两实数,
为两实数,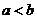 且
且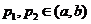 ,若
,若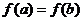 ,求证:
,求证: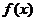 在区间
在区间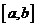 上的单调增区间的长度和为
上的单调增区间的长度和为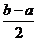 (闭区间
(闭区间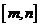 的长度定义为
的长度定义为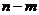 )。
)。
13.(2008·广东卷理19)设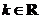 ,函数
,函数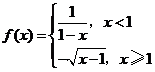 ,
,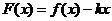 ,
,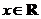 ,试讨论函数
,试讨论函数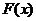 的单调性.
的单调性.
12. (2009·浙江理14)某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下:
|
高峰时间段用电价格表 |
低谷时间段用电价格表 |
||
|
高峰月用电量 (单位:千瓦时) |
高峰电价 (单位:元/千瓦时) |
低谷月用电量 (单位:千瓦时) |
低谷电价 (单位:元/千瓦时) |
|
50及以下的部分 |
0.568 |
50及以下的部分 |
0.288 |
|
超过50至200的部分 |
0.598 |
超过50至200的部分 |
0.318 |
|
超过200的部分 |
0.668 |
超过200的部分 |
0.388 |
若某家庭5月份的高峰时间段用电量为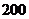 千瓦时,低谷时间段用电量为
千瓦时,低谷时间段用电量为 千瓦时,则按这种计费方式该家庭本月应付的电费为
元(用数字作答).
千瓦时,则按这种计费方式该家庭本月应付的电费为
元(用数字作答).
10.( 2009·山东文理14)若函数f(x)=a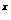 -x-a(a>0且a
-x-a(a>0且a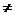 1)有两个零点,则实数a的取值范围是 .
1)有两个零点,则实数a的取值范围是 . 
 11.( 2009·山东文理16)已知定义在R上的奇函数
11.( 2009·山东文理16)已知定义在R上的奇函数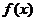 ,满足
,满足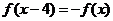 ,且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间
,且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间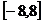 上有四个不同的根
上有四个不同的根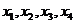 ,则
,则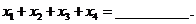


9.( 2009·山东文10)定义在R上的函数f(x)满足f(x)=
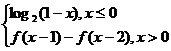 ,则f(2009)的值为
,则f(2009)的值为
8.( 2009·宁夏海南文12)用min{a,b,c}表示a,b,c三个数中的最小值。
设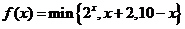 (x
(x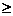 0),则
0),则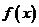 的最大值为
的最大值为
7.( 2009·辽宁理12)若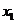 满足
满足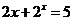 ,
,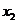 满足
满足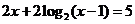 ,则
,则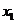 +
+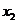 =
=
6.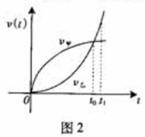 (
2009·广东理8)已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为
(
2009·广东理8)已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为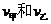 (如图2所示).那么对于图中给定的
(如图2所示).那么对于图中给定的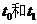 ,下列判断中一定正确的是
,下列判断中一定正确的是
A.在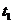 时刻,甲车在乙车前面
时刻,甲车在乙车前面 
 B
B 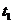 时刻后,甲车在乙车后面
时刻后,甲车在乙车后面
C.在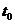 时刻,两车的位置相同 D.
时刻,两车的位置相同 D. 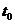 时刻后,乙车在甲车前面
时刻后,乙车在甲车前面
5.( 2009·福建文11).若函数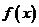 的零点与
的零点与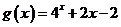 的零点之差的绝对值不超过0.25, 则
的零点之差的绝对值不超过0.25, 则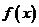 可以是
可以是
A. 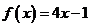 B.
B. 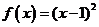

C.  D.
D. 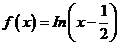
4.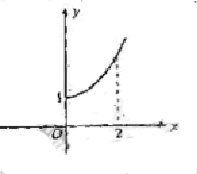 ( 2009·福建文8).定义在R上的偶函数
( 2009·福建文8).定义在R上的偶函数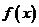 的部分图像如右图所示,则在
的部分图像如右图所示,则在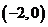 上,下列函数中与
上,下列函数中与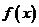 的单调性不同的是
的单调性不同的是
A.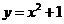 B.
B. 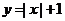
C. 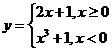
D.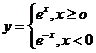
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com