
1. 若集合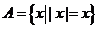 ,
,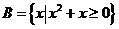 ,则
,则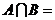 .
.
20.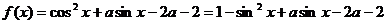
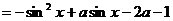
(I)当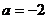 时,由
时,由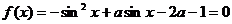 得
得
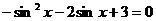 ,
,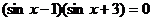 ,所以
,所以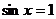 ,则
,则
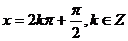 ,所以满足
,所以满足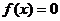 的x值是
的x值是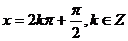
(Ⅱ)令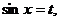 则
则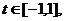 由
由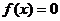 有实数解等价于方程
有实数解等价于方程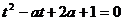 在
在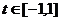 上有解,记
上有解,记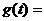
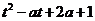
①
若方程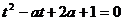 在
在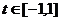 上有一解,则
上有一解,则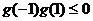 ,
,
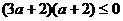 得
得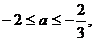
②
若方程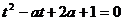 在
在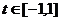 上有两解,则
上有两解,则

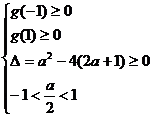 ,即
,即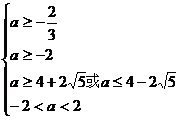 解得
解得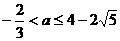 .
.
综合①.②得所求a的取值范是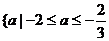 或
或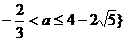 即
即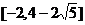
(Ⅲ)由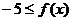 对
对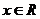 恒成立,得
恒成立,得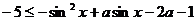 对
对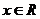 恒成立,
恒成立,
即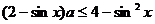 对
对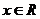 恒成立,又
恒成立,又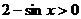 恒成立,所以
恒成立,所以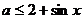 对
对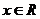 恒成立,
恒成立, 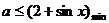 又
又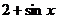 的值域为
的值域为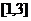 ,∴
,∴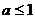 .
.
由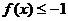 对
对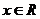 恒成立,得
恒成立,得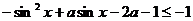 对
对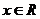 恒成立,
恒成立,
即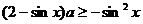 对
对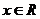 恒成立,又
恒成立,又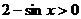 恒成立,
恒成立,
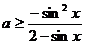 对
对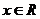 恒成立,所以
恒成立,所以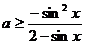 的最大值,又
的最大值,又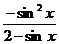 最大值为0,
最大值为0,
所以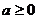 ,综上所述,对任意
,综上所述,对任意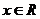 都有
都有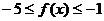 成立的a的取值范围是
成立的a的取值范围是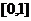 .
.
19.(1) 由题意得: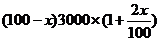
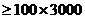 ,
,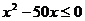 ,
,
解得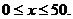 又
又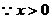 ,
,
(2)设这100万农民的人均年收入为y元,则
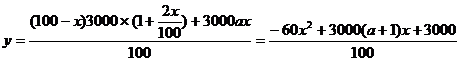
即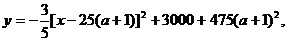
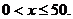
当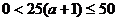 且
且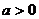 ,即
,即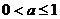 时, 则
时, 则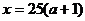 时,y最大.
时,y最大.
当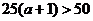 即
即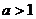 时, 则y在
时, 则y在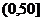 单调递增,∴当
单调递增,∴当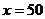 时,y取最大值.
时,y取最大值.
答: 在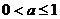 时, 安排
时, 安排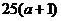 万人进入企业工作,在
万人进入企业工作,在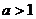 时安排50万人进入企业工
时安排50万人进入企业工
作,才能使这100万人的人均年收入最大.
18.(I)因为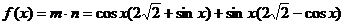
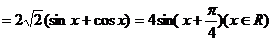 ∴
∴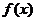 的最大值是4.
的最大值是4.
(2)∵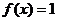 ,∴
,∴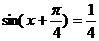 ,又
,又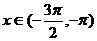 ,即
,即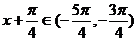 ,
,
所以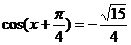 ,
,
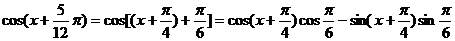
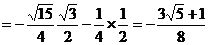 .
.
17.(1)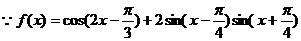
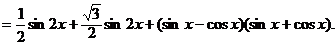
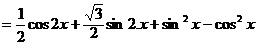

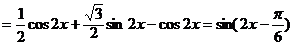
由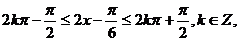 得
得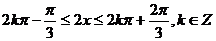
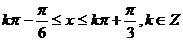 ,∴单调递增区间为:
,∴单调递增区间为: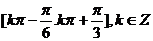
由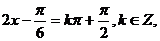 得:
得: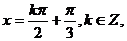 对称轴方程为
对称轴方程为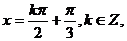
(2)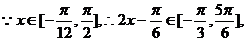 因为
因为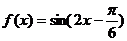
在区间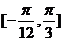 上单调递增.在区间
上单调递增.在区间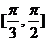 单调递减,所以当
单调递减,所以当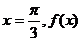 取最大值l.
取最大值l.
又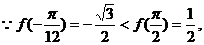 当
当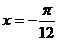 时,
时,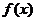 取最小值
取最小值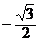
所以函数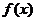 在区间上的值域为
在区间上的值域为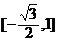 .
.
16.(1)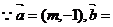
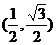 ,且
,且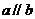 ,∴
,∴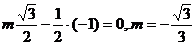
(2)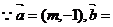
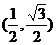 ,且
,且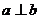 ,∴
,∴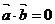 ,
,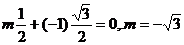 .
.
(3)∵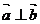 ,∴
,∴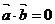 ,由(2)可知
,由(2)可知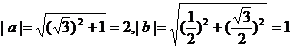
由条件得: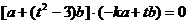
即: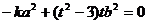 ,
,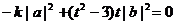 ,
,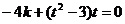
∴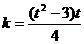 ,故:
,故: 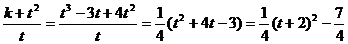
当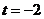 时,
时,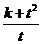 有最小值
有最小值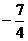 .
.
15.∵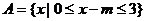 ,∴
,∴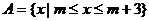 ,
,
(1)当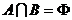 时,有
时,有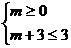 ,解得
,解得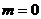
(2)当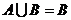 时,则
时,则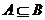 ,∴有
,∴有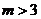 或
或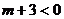 ,解得
,解得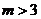 或
或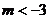
11.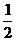 12
12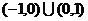 13.1
14.
13.1
14.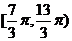
6.7
7. 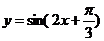 8.一
9.
8.一
9. 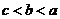 10.
10.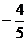
1.-3 2.10
3. 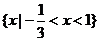 4. 1.56 5.2
4. 1.56 5.2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com