
3.( 2009·福建理10).函数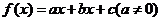 的图象关于直线
的图象关于直线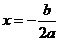 对称。据此可推测,对任意的非零实数a,b,c,m,n,p,关于x的方程
对称。据此可推测,对任意的非零实数a,b,c,m,n,p,关于x的方程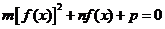 的解集都不可能是
的解集都不可能是
A. 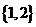 B
B
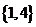 C
C
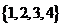 D
D 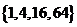
2.设函数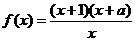 为奇函数,则
为奇函数,则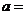 .
.
1.设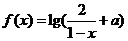 是奇函数,则使
是奇函数,则使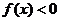 的
的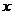 的取值范围是
的取值范围是
13.解法一:
(I)由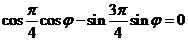 得
得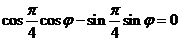
即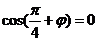 又
又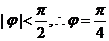


(Ⅱ)由(I)得,
依题意,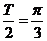
又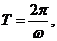 故
故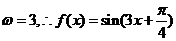
函数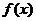 的图像向左平移
的图像向左平移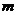 个单位后所对应的函数为
个单位后所对应的函数为
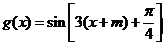
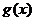 是偶函数当且仅当
是偶函数当且仅当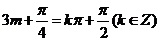
即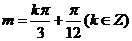
从而,最小正实数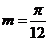
解法二:
(I)同解法一
(Ⅱ)由(I)得,

依题意,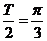


又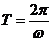 ,故
,故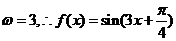
函数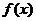 的图像向左平移
的图像向左平移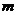 个单位后所对应的函数为
个单位后所对应的函数为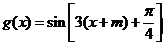
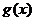 是偶函数当且仅当
是偶函数当且仅当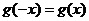 对
对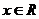 恒成立
恒成立
亦即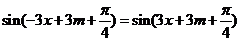 对
对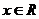 恒成立。
恒成立。
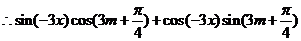
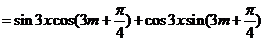
即 对
对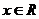 恒成立。
恒成立。
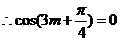
故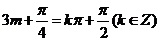
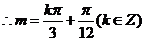


从而,最小正实数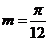
12.[解析] 本小题主要考查向量的基本概念,同时考查同角三角函数的基本关系式、二倍角的正弦、两角和的正弦与余弦公式,考查运算和证明得基本能力。满分14分。
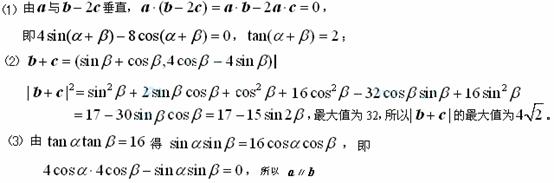
11. 解: (1)f(x)=cos(2x+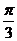 )+sin
)+sin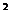 x.=
x.=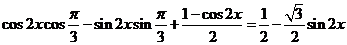
所以函数f(x)的最大值为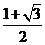 ,最小正周期
,最小正周期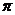 .
. 

(2)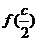 =
=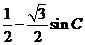 =-
=-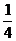 , 所以
, 所以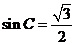 , 因为C为锐角, 所以
, 因为C为锐角, 所以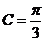 ,
,
又因为在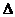 ABC 中, cosB=
ABC 中, cosB=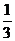 ,
所以
,
所以 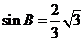 , 所以
, 所以 

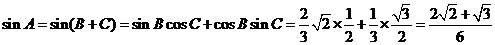 .
.
[命题立意]:本题主要考查三角函数中两角和差的弦函数公式、二倍角公式、三角函数的性质以及三角形中的三角关系.
10.解: (1)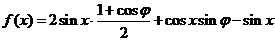
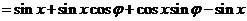
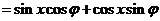
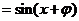
因为函数f(x)在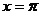 处取最小值,所以
处取最小值,所以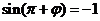 ,由诱导公式知
,由诱导公式知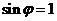 ,因为
,因为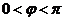 ,所以
,所以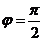 .所以
.所以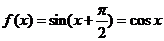


(2)因为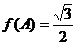 ,所以
,所以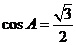 ,因为角A为
,因为角A为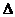 ABC的内角,所以
ABC的内角,所以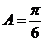 .又因为
.又因为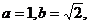 所以由正弦定理,得
所以由正弦定理,得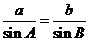 ,也就是
,也就是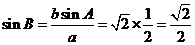 ,因为
,因为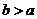 ,所以
,所以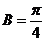 或
或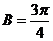 .
.
当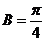 时,
时,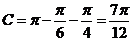 ;当
;当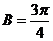 时,
时,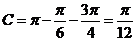 .
.
[命题立意]:本题主要考查了三角函数中两角和差的弦函数公式、二倍角公式和三角函数的性质,并利用正弦定理解得三角形中的边角.注意本题中的两种情况都符合.
9.解:(1)∵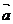 与
与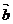 互相垂直,则
互相垂直,则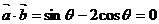 ,即
,即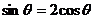 ,代入
,代入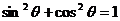 得
得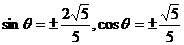 ,又
,又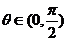 ,∴
,∴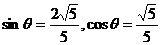 .
.
(2)∵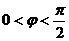 ,
,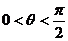 ,∴
,∴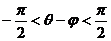 ,则
,则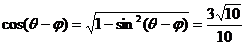 ,∴
,∴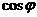
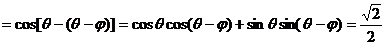 .
.
7. [解析](1)依题意有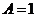 ,则
,则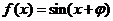 ,将点
,将点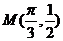 代入得
代入得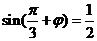 ,
,
而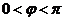 ,
,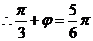 ,
,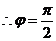 ,故
,故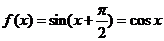 ;
;
(2)依题意有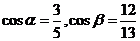 ,而
,而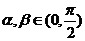 ,
,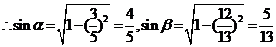 ,
,
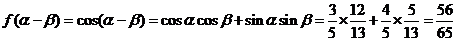 。
。
8[解析]本小题考查三角函数的定义、两角和的正切、二倍角的正切公式。由条件得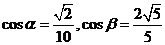 ,
, 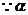 为锐角,故
为锐角,故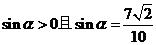 。同理可得
。同理可得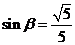 ,
,
因此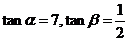 。(1)
。(1)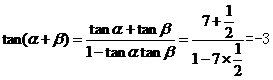 。
。
(2)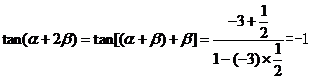 ,
,
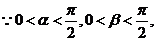
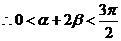 ,从而
,从而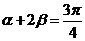 。
。
6.[解析](Ⅰ)f(x)=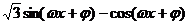 =
=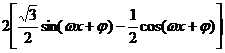
=2sin(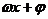 -
-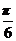 ),因为f(x)为偶函数,所以对x∈R,f(-x)=f(x)恒成立,
),因为f(x)为偶函数,所以对x∈R,f(-x)=f(x)恒成立,
因此sin(-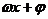 -
-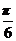 )=sin(
)=sin(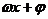 -
-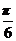 ).
).
即-sin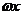 cos(
cos(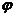 -
-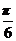 )+cos
)+cos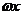 sin(
sin(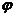 -
-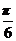 )=sin
)=sin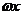 cos(
cos(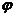 -
-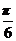 )+cos
)+cos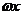 sin(
sin(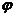 -
-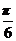 ),
),
整理得 sin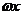 cos(
cos(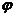 -
-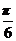 )=0.因为
)=0.因为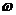 >0,且x∈R,所以cos(
>0,且x∈R,所以cos(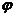 -
-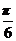 )=0.
)=0.
又因为0<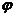 <π,故
<π,故 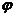 -
-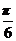 =
=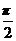 .所以f(x)=2sin(
.所以f(x)=2sin(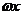 +
+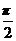 )=2cos
)=2cos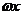 .由题意得
.由题意得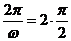 ,所以
,所以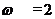
故 f(x)=2cos2x.因为 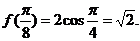
(Ⅱ)将f(x)的图象向右平移个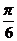 个单位后,得到
个单位后,得到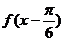 的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到
的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到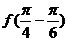 的图象.所以
的图象.所以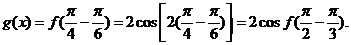
当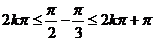 (k∈Z),,即4kπ+≤
(k∈Z),,即4kπ+≤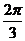 ≤x≤4kπ+
≤x≤4kπ+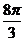 (k∈Z)时,g(x)单调递减.
(k∈Z)时,g(x)单调递减.
因此g(x)的单调递减区间为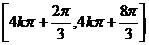 (k∈Z)
(k∈Z)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com