
11. 解析:因为定义在R上的奇函数,满足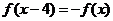 ,所以
,所以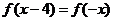 ,所以, 由
,所以, 由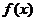 为奇函数,所以函数图象关于直线
为奇函数,所以函数图象关于直线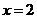 对称且
对称且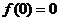 ,由
,由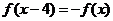 知
知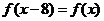 ,所以函数是以8为周期的周期函数,又因为
,所以函数是以8为周期的周期函数,又因为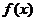 在区间[0,2]上是增函数,所以
在区间[0,2]上是增函数,所以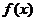 在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间
在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间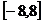 上有四个不同的根
上有四个不同的根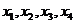 ,不妨设
,不妨设 由对称性知
由对称性知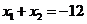
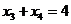 所以
所以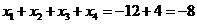
10. 解析:设函数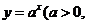 且
且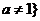 和函数
和函数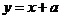 ,则函数f(x)=a
,则函数f(x)=a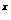 -x-a(a>0且a
-x-a(a>0且a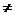 1)有两个零点,
就是函数
1)有两个零点,
就是函数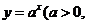 且
且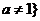 与函数
与函数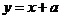 有两个交点,由图象可知当
有两个交点,由图象可知当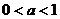 时两函数只有一个交点,不符合,当
时两函数只有一个交点,不符合,当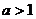 时,因为函数
时,因为函数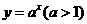 的图象过点(0,1),而直线
的图象过点(0,1),而直线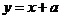 所过的点(0,a)一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是
所过的点(0,a)一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是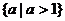
9. 解析:由已知得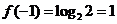 ,
,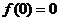 ,
,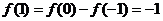 ,
,
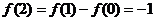 ,
,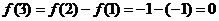 ,
,
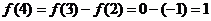 ,
,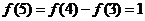 ,
,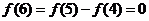 ,
,
所以函数f(x)的值以6为周期重复性出现.,所以f(2009)= f(5)=1,故选C.
8.解析:画出y=2x,y=x+2,y=10-x的图象,如右图,观察图象可知,当0≤x≤2时,f(x)=2x,当2≤x≤3时,f(x)=x+2,当x>4时,f(x)=10-x,f(x)的最大值在x=4时取得为6,故选C。.
7.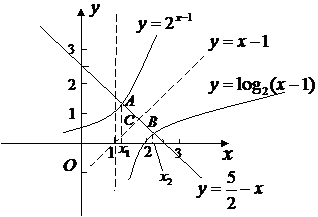 解析:
解析: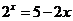 ,
,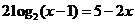 ,
,
即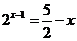 ,
,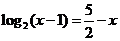 ,
,
作出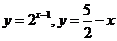 ,
,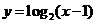 的图像(如图),
的图像(如图),
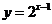 与
与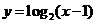 的图像关于
的图像关于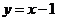 对称,
对称,
它们与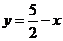 的交点A、B的中点为
的交点A、B的中点为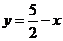 与
与
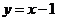 的交点C,
的交点C,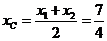 ,∴
,∴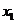 +
+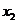 =
=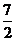 。
。
6. 解析:由图像可知,曲线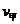 比
比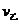 在0-
在0-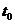 、0-
、0-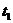 与
与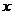 轴所围成图形面积大,则在
轴所围成图形面积大,则在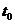 、
、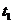 时刻,甲车均在乙车前面,选A.
时刻,甲车均在乙车前面,选A.
5. 解析: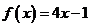 的零点为x=
的零点为x=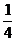 ,
,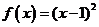 的零点为x=1,
的零点为x=1,
 的零点为x=0,
的零点为x=0,
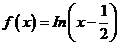 的零点为x=
的零点为x=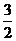 .现在我们来估算
.现在我们来估算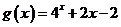 的零点,因为g(0)=
-1,g(
的零点,因为g(0)=
-1,g( )=1,所以g(x)的零点x
)=1,所以g(x)的零点x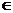 (0,
(0,
 ),又函数
),又函数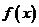 的零点与
的零点与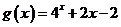 的零点之差的绝对值不超过0.25,只有
的零点之差的绝对值不超过0.25,只有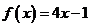 的零点适合,故选A。
的零点适合,故选A。
4. 解析:根据偶函数在关于原点对称的区间上单调性相反,故可知求在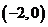 上单调递减,注意到要与
上单调递减,注意到要与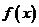 的单调性不同,故所求的函数在
的单调性不同,故所求的函数在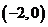 上应单调递增。而函数
上应单调递增。而函数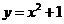 在
在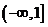 上递减;函数
上递减;函数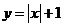 在
在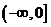 时单调递减;函数
时单调递减;函数
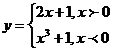 在(
在(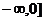 上单调递减,理由如下y’=3x2>0(x<0),故函数单调递增,显然符合题意;而函数
上单调递减,理由如下y’=3x2>0(x<0),故函数单调递增,显然符合题意;而函数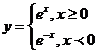 ,有y’=-
,有y’=-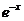 <0(x<0),故其在(
<0(x<0),故其在(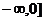 上单调递减,不符合题意,综上选C。
上单调递减,不符合题意,综上选C。
3. 答案:D
15.(2009·江苏19)(本小题满分16分)
按照某学者的理论,假设一个人生产某产品单件成本为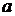 元,如果他卖出该产品的单价为
元,如果他卖出该产品的单价为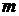 元,则他的满意度为
元,则他的满意度为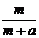 ;如果他买进该产品的单价为
;如果他买进该产品的单价为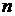 元,则他的满意度为
元,则他的满意度为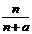 .如果一个人对两种交易(卖出或买进)的满意度分别为
.如果一个人对两种交易(卖出或买进)的满意度分别为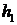 和
和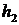 ,则他对这两种交易的综合满意度为
,则他对这两种交易的综合满意度为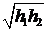 .
.
现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为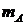 元和
元和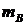 元,甲买进A与卖出B的综合满意度为
元,甲买进A与卖出B的综合满意度为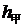 ,乙卖出A与买进B的综合满意度为
,乙卖出A与买进B的综合满意度为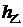

(1)求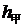 和
和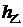 关于
关于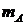 、
、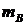 的表达式;当
的表达式;当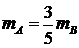 时,求证:
时,求证: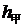 =
=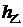 ;
;
(2)设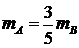 ,当
,当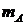 、
、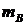 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
(3)记(2)中最大的综合满意度为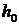 ,试问能否适当选取
,试问能否适当选取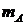 、
、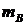 的值,使得
的值,使得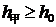 和
和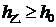 同时成立,但等号不同时成立?试说明理由。
同时成立,但等号不同时成立?试说明理由。
函数答案
1.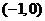 2.
2. 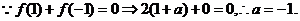
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com