
1、观察果蝇(2n=8)的生殖腺细胞,正常情况下不可能看到
A.卵巢的某些细胞中有16条染色体 B.卵巢的某些细胞中没有同源染色体
C.精巢的某些细胞中有8个四分体 D.精巢的某些细胞中没有X染色体
24、(1)胸腺嘧啶脱氧核苷酸 尿嘧啶核糖核苷酸 (2)分生区 线粒体
(3)ATP(能量) 2︰1︰2 后 (4)a、c 蛋白质
(5)b d、e (6)分裂期时间远远短于分裂间期时间
23、(1)TaqDNA聚合酶 一小段DNA或RNA 与模板结合,使DNA聚合酶从引物3’端延伸DNA链
(2)引物通过碱基互补与DNA模板链结合 对照组不加DNA模板,其它条件相同
(3)同一种DNA限制性内切酶 磷酸二酯键
(4)小型环状DNA
(5)红霉素抗性基因 红霉素
22、答案:(1)CH2O2 (1分),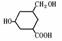 (2分)
(2分)
(2)加成反应(1分),羟基(酚羟基)、羧基、醛基(2分)
(3)1∶2∶1 (2分)
(4) (2分)
(2分)
(5)4 (2分),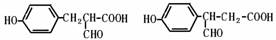
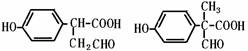 (2分,任意一个)
(2分,任意一个)
(6)C6H12O6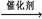 2C2H5OH + 2CO2(2分)
2C2H5OH + 2CO2(2分)
21、(1)a、d、e、h、j(漏选或错选得0分)
(2)100mL的容量瓶
(3)酸碱指示剂(填“甲基橙”或“酚酞”给1分,填“石蕊”得0分)
(4)b (5)F;溶解、过滤和洗涤(答出“溶解“过滤”“洗涤”即得4分)
20、(1)甲为:SiO2 乙为:Na2SiO3
丁为:Al(OH)3 (写名称也可)
(2)O2 ;丙的电子式:H︰O︰H
(3)Si +2NaOH +H2O == Na2SiO3 +2H2↑
(4)AlO2-+4H+= Al3++2H2O (由于没有注明,写离子方程式也可)
19、

18、解答(1)(4分)上升时间 上升高度
上升高度
判断当速度达到350m/s时,下落高度 ,此时离地高度为h+h上-h下=7000+2000-6125=2875>2000m,
,此时离地高度为h+h上-h下=7000+2000-6125=2875>2000m, ,所以一次上下创造的完全失重的时间为55s
,所以一次上下创造的完全失重的时间为55s
(2)(4分)当飞机在离地4500m>2875m,所以飞机仍在完全失重状态,飞机自由下落的高度 推力
推力 -
-
(3)(4分)为了节约能量,那么让飞机在2000m是速度正好为350m/s,所以此时最大离地高度为2000+h下=8125m,故飞机拉起的高度为8125-h上=6125m,即比原来提前Δh=7000-6125=875m拉起,飞机节省的能量就是在这875m中克服重力和阻力做的功之和(因为在这个过程飞机是匀速的,动能没有改变)
17、⑴
⑵测量步骤如下: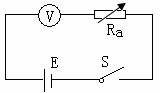
③调节电阻箱Ra电阻值,使得电压表满偏,记下此时Ra的值R1。
④增大Ra的值,使得电压表半偏,记下此时Ra的值R2,
计算电压表内阻的公式:Rv=R2-2R1
25.(2009全国卷Ⅱ文)(本小题满分12分)
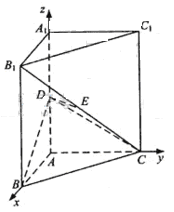
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1
(Ⅰ)证明:AB=AC
(Ⅱ)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小
解析:本题考查线面垂直证明线面夹角的求法,第一问可取BC中点F,通过证明AF⊥平面BCC1,再证AF为BC的垂直平分线,第二问先作出线面夹角,即证四边形AFED是正方形可证平面DEF⊥平面BDC,从而找到线面夹角求解。此题两问也可建立空间直角坐标系利用向量法求解。
解法一:(Ⅰ)取BC中点F,连接EF,则EF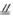
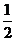
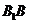 ,从而EF
,从而EF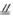 DA。
DA。

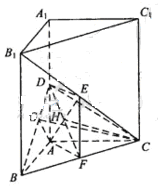
连接AF,则ADEF为平行四边形,从而AF//DE。又DE⊥平面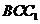 ,故AF⊥平面
,故AF⊥平面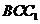 ,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC。
,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC。
(Ⅱ)作AG⊥BD,垂足为G,连接CG。由三垂线定理知CG⊥BD,故∠AGC为二面角A-BD-C的平面角。由题设知,∠AGC=600..
设AC=2,则AG=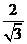 。又AB=2,BC=
。又AB=2,BC=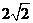 ,故AF=
,故AF=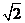 。
。
由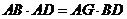 得2AD=
得2AD=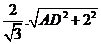 ,解得AD=
,解得AD=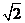 。
。
故AD=AF。又AD⊥AF,所以四边形ADEF为正方形。
因为BC⊥AF,BC⊥AD,AF∩AD=A,故BC⊥平面DEF,因此平面BCD⊥平面DEF。
连接AE、DF,设AE∩DF=H,则EH⊥DF,EH⊥平面BCD。
连接CH,则∠ECH为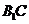 与平面BCD所成的角。
与平面BCD所成的角。
 因ADEF为正方形,AD=
因ADEF为正方形,AD=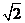 ,故EH=1,又EC=
,故EH=1,又EC=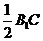 =2,
=2,
所以∠ECH=300,即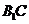 与平面BCD所成的角为300.
与平面BCD所成的角为300.
解法二:
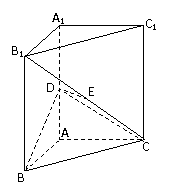
(Ⅰ)以A为坐标原点,射线AB为x轴的正半轴,建立如图所示的直角坐标系A-xyz。
设B(1,0,0),C(0,b,0),D(0,0,c),则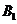 (1,0,2c),E(
(1,0,2c),E(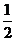 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com