
1.
已知曲线C: 的横坐标分别为1和
的横坐标分别为1和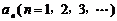 ,且a1=5,数列{xn}满足xn+1 = tf (xn –
1) + 1(t > 0且
,且a1=5,数列{xn}满足xn+1 = tf (xn –
1) + 1(t > 0且 ).设区间
).设区间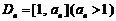 ,当
,当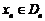 时,曲线C上存在点
时,曲线C上存在点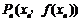 使得xn的值与直线AAn的斜率之半相等.
使得xn的值与直线AAn的斜率之半相等.
(1)
证明: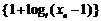 是等比数列;
是等比数列;
(2)
当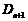
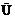
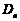 对一切
对一切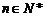 恒成立时,求t的取值范围;
恒成立时,求t的取值范围;
(3) 记数列{an}的前n项和为Sn,当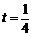 时,试比较Sn与n + 7的大小,并证明你的结论.
时,试比较Sn与n + 7的大小,并证明你的结论.
解:(1) ∵由已知得 ∴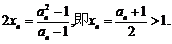
由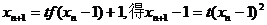
∴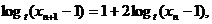 即
即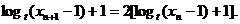
∴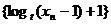 是首项为
是首项为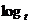 2+1为首项,公比为2的等比数列. ······ 4分
2+1为首项,公比为2的等比数列. ······ 4分
(2) 由(1)得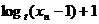 =(
=(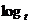 2+1)·2n-1,∴
2+1)·2n-1,∴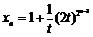
从而an=2xn-1=1+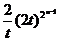 ,由Dn+1
,由Dn+1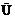 Dn,得an+1<an,即
Dn,得an+1<an,即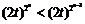 .
.
∴0<2t<1,即0<t<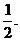 ··············································································· 9分
··············································································· 9分
(3) 当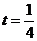 时,
时,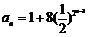
∴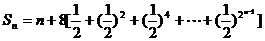
不难证明:当n≤3时,2n-1≤n+1;当n≥4时,2n-1>n+1.
∴当n≤3时,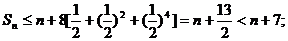
当n≥4时,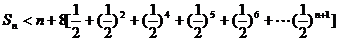
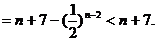
综上所述,对任意的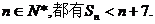 ·········································· 13分
·········································· 13分
9.(西南师大附中高2010级第四次月考)
2.解(1)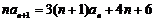 ,两边同除以
,两边同除以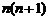 得:
得:
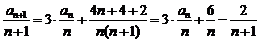
∴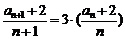
∴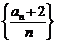 是首项为
是首项为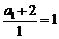 ,公比
,公比 的等比数列………………4分
的等比数列………………4分
∴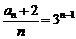
∴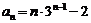
(2)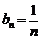 ,当
,当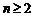 时,
时,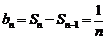 ,
,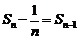 ………………5分
………………5分
两边平方得: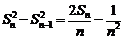
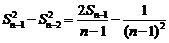
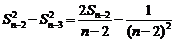
……
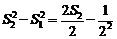
相加得: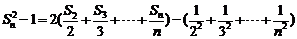
又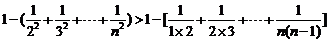
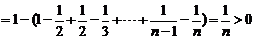
∴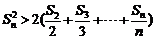 …………………………………………9分
…………………………………………9分
(3)(数学归纳法)
当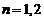 时,显然成立
时,显然成立
当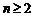 时,证明加强的不等式
时,证明加强的不等式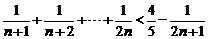
假设当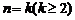 时命题成立,即
时命题成立,即
则当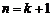 时
时
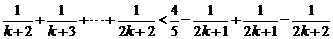
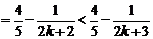
∴当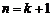 时命题成立,故原不等式成立……………………14分
时命题成立,故原不等式成立……………………14分
1.解(1)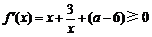 对
对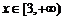 恒成立……………1分
恒成立……………1分
∴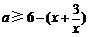 又
又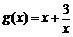 在
在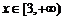 为单调递增函数
为单调递增函数
∴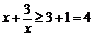 ∴
∴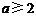 …………………………………5分
…………………………………5分
(2)设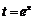 ,
,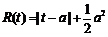
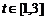
当 时,
时,
∴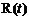 最小值为
最小值为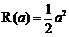 ………………………………………9分
………………………………………9分
当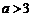 时,
时,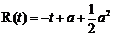 ,
,
∴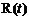 最小值为
最小值为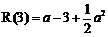 ………………………………12分
………………………………12分
综上,当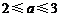 时,
时,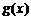 最小值为
最小值为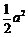 ,
,
当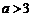 时,
时,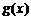 最小值为
最小值为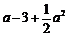
2.数列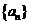 满足
满足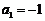 ,
,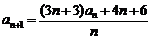 .
.
(1)求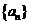 通项公式
通项公式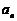 ;
;
(2)令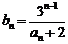 ,数列
,数列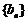 前
前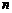 项和为
项和为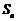 ,
,
求证:当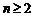 时,
时,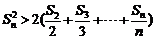 ;
;
(3)证明: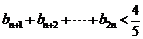 .
.
1.已知函数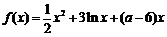 在
在 上是增函数.
上是增函数.
(1)求实数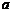 的取值范围;
的取值范围;
(2)在(1)的结论下,设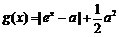 ,
,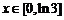 ,求函数
,求函数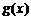 最小值.
最小值.
8.(江西师大附中、临川一中、南昌三中2010届高三联考理科)
2.(1)取p=n,q=1,则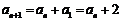 …………(2分)
…………(2分)
∴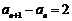 (
(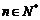 )
)
∴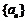 是公差为2,首项为2的等差数列
是公差为2,首项为2的等差数列
∴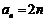 …………(4分)
…………(4分)
(2)∵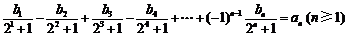 ①
①
∴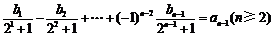 ②
②
①-②得: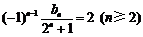 …………(5分)
…………(5分)
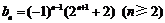 …………(6分)
…………(6分)
当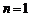 时,
时, ∴
∴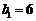 满足上式 …………(7分)
满足上式 …………(7分)
∴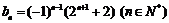 …………(8分)
…………(8分)
(3)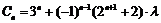
假设存在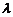 ,使
,使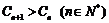
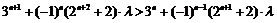
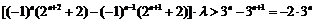
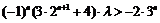 …………(9分)
…………(9分)
当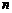 为正偶函数时,
为正偶函数时, 恒成立
恒成立
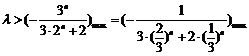
当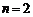 时
时
∴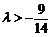 …………(11分)
…………(11分)
当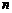 为正奇数时,
为正奇数时,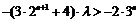 恒成立
恒成立
∴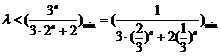
当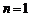 时
时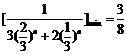
∴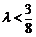 …………(13分)
…………(13分)
综上,存在实数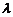 ,且
,且 …………(14分)
…………(14分)
1.(1)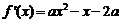 …………(1分)
…………(1分)
当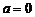 时,
时, …………(2分)
…………(2分)
当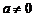 时,
时,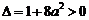 ,方程
,方程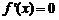 有不相等的两根为
有不相等的两根为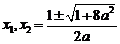
…………(3分)
 当
当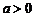 时,
时,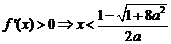 或
或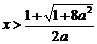 ……(4分)
……(4分)
 当
当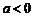 时,
时,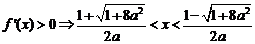 …………(5分)
…………(5分)
综上:当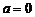 时,
时,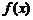 在
在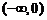 上递增
上递增
当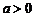 时,
时,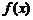 在
在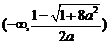 、
、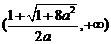 上递增
上递增
当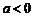 时,
时,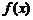 在
在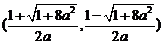 上递增 ……(6分)
上递增 ……(6分)
(2)∵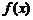 在
在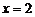 处有极值,∴
处有极值,∴ ,∴
,∴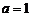 …………(7分)
…………(7分)
令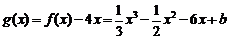
∴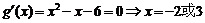 …………(8分)
…………(8分)
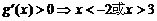
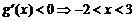
∴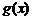 在
在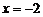 处有极大值,在
处有极大值,在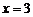 处有极小值 …………(9分)
处有极小值 …………(9分)
要使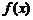 图象与
图象与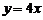 有三个公共点
有三个公共点
则 …………(11分)
…………(11分)
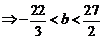 ,即
,即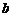 的取值范围为
的取值范围为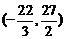 …………(12分)
…………(12分)
2.已知数列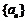 中,
中,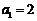 ,对于任意的
,对于任意的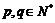 ,有
,有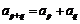
(1)求数列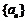 的通项公式;
的通项公式;
(2)若数列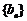 满足:
满足: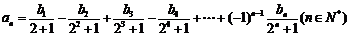 求数列
求数列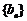 的通项公式;
的通项公式;
(3)设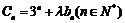 ,是否存在实数
,是否存在实数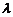 ,当
,当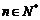 时,
时,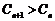 恒成立,若存在,求实数
恒成立,若存在,求实数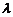 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com