
1.解:(1)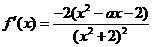 ……………………………………………1分
……………………………………………1分
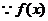 在
在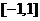 上是增函数
上是增函数
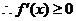 即
即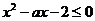 ,在
,在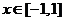 恒成立 …………① …………3分
恒成立 …………① …………3分
设 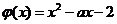 ,则由①得
,则由①得
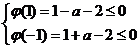 解得
解得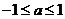
所以,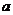 的取值范围为
的取值范围为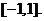 ………………………………………………………6分
………………………………………………………6分
(2)由(1)可知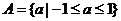
由 即
即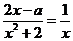 得
得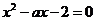
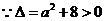
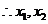 是方程
是方程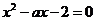 的两个非零实根
的两个非零实根
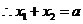 ,
,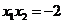 ,又由
,又由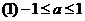
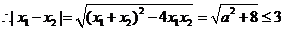 ……………………………9分
……………………………9分
于是要使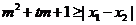 对
对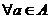 及
及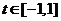 恒成立
恒成立
即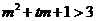 即
即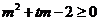 对
对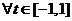 恒成立 ………②………11分
恒成立 ………②………11分
 设
设 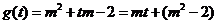 ,则由②得
,则由②得
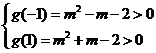 解得
解得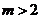 或
或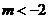
故存在实数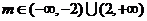 满足题设条件…………………………14分
满足题设条件…………………………14分
2解:(1)由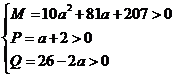 得
得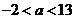 ……………2分
……………2分
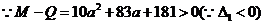 ………………………3分
………………………3分
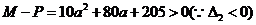 ………………………4分
………………………4分
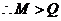 ,
,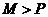
又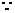 当
当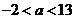 时,
时,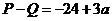 ,
,
当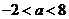 时,即
时,即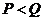 ,则
,则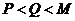 ………………………5分
………………………5分
当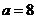 时,
时,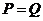 ,则
,则
当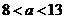 时,
时,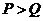 ,则
,则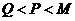
(2)依题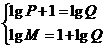 即
即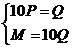
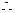
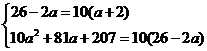
解得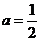 ,从而
,从而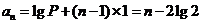 ………………………9分
………………………9分
(3) ,设
,设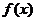 与
与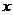 轴交点为
轴交点为
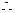 当
当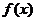 =0时有
=0时有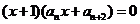
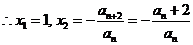 ………………………………………11分
………………………………………11分

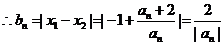
又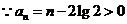 ,
,
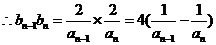
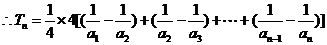
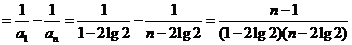 …………14分
…………14分
2. 设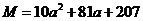 ,
,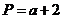 ,Q=
,Q=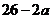 ;若将
;若将 ,
,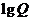 ,
,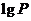 适当排序后可构成公差为1的等差数列
适当排序后可构成公差为1的等差数列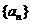 的前三项
的前三项
 (I)在使得
(I)在使得 ,
,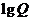 ,
,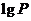 有意义的条件下,试比较
有意义的条件下,试比较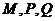 的大小;
的大小;
(II)求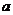 的值及数列
的值及数列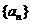 的通项;
的通项;
(III)记函数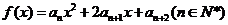 的图象在
的图象在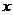 轴上截得的线段长为
轴上截得的线段长为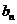 ,设
,设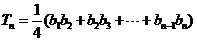 ,求
,求 .
.
1.已知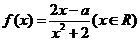 在区间
在区间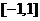 上是增函数
上是增函数
(I)求实数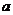 的取值范围;
的取值范围;
(II)记实数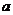 的取值范围为集合A,且设关于
的取值范围为集合A,且设关于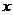 的方程
的方程 的两个非零实根为
的两个非零实根为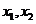 。
。
①求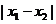 的最大值;
的最大值;
②试问:是否存在实数m,使得不等式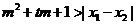 对
对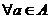 及
及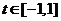 恒成立?若存在,求m的取值范围;若不存在,请说明理由.
恒成立?若存在,求m的取值范围;若不存在,请说明理由.
2.(广东省东华高级中学2010届高三上学期摸底考试)
2.解:(1)由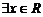 ,
,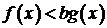 ,得
,得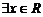 ,
,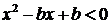 ,……………1分
,……………1分
所以,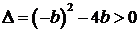

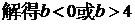 ;……………4分
;……………4分
(2)由题设得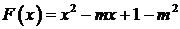 ,……………5分
,……………5分
对称轴方程为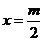 ,
,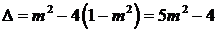 。……………7分
。……………7分
由于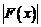 在
在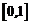 上单调递增,则有
上单调递增,则有
(Ⅰ)当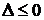 即
即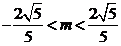 时,有
时,有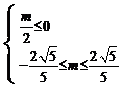
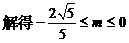 。……………9分
。……………9分
(Ⅱ)当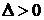 即
即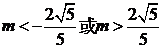 时,设方程
时,设方程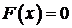 的根为
的根为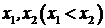 ,
,
① 若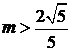 ,则
,则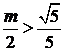 ,有
,有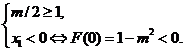
解得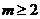 ;……………11分
;……………11分
② 若 ,即
,即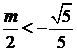 ,有
,有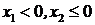 ;
;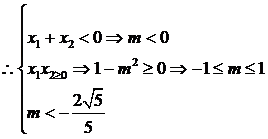
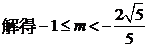 。……………13分由①②得
。……………13分由①②得 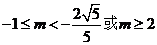 。
。
综合(Ⅰ), (Ⅱ)有 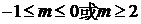 .……………14分
.……………14分
1.解:(1)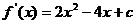 ,………1分
,………1分
依题意,有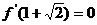 ,即
,即 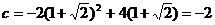 .……………2分
.……………2分
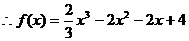 ,
,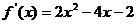 .
.
令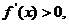 得
得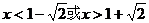 ,……………4分
,……………4分
从而f(x)的单调增区间为: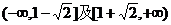 ;……………5分
;……………5分
(2)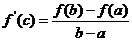 ;……………8分
;……………8分
(3)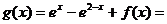
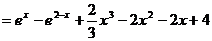 ,…………9分
,…………9分
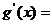
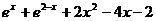 ……………10分
……………10分
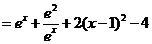
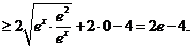 ………12分
………12分
由(2)知,对于函数y=g(x)图象上任意两点A、B,在A、B之间一定存在一点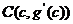 ,使得
,使得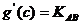 ,又
,又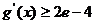 ,故有
,故有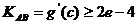 ,证毕.………14分
,证毕.………14分
2. 已知函数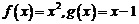 .
.
(1)若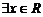 使
使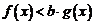 ,求实数
,求实数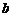 的取值范围;
的取值范围;
(2)设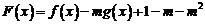 ,且
,且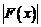 在
在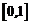 上单调递增,求实数
上单调递增,求实数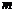 的取值范围.
的取值范围.
1. 已知
已知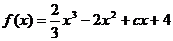 ,
,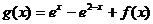 ,
,
(1)若f(x)在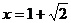 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间;
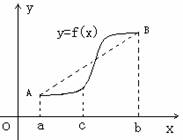
(2)如右图所示,若函数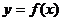 的图象在
的图象在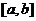 连续光滑,试猜想拉格朗
日中值定理:即一定存在
连续光滑,试猜想拉格朗
日中值定理:即一定存在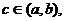 使得
使得 ?
?
(用含有a,b,f(a),f(b)的表达式直接回答)
(3)利用(2)证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
1.(广东省中山五中2010届高三第四次月考)
33.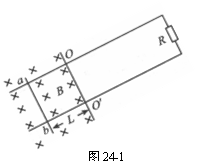 (13分)如图24-1所示,相距为L的光滑平行金属导轨与水平间的夹角为
(13分)如图24-1所示,相距为L的光滑平行金属导轨与水平间的夹角为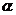 ,导轨一部分处在垂直导轨平面的匀强磁场中,OO’为磁场边界,磁感应强度为B,导轨右侧接有定值电阻R,导轨电阻忽略不计。在距OO’为L处垂直导轨放置一质量为m、电阻不计的金属杆ab。
,导轨一部分处在垂直导轨平面的匀强磁场中,OO’为磁场边界,磁感应强度为B,导轨右侧接有定值电阻R,导轨电阻忽略不计。在距OO’为L处垂直导轨放置一质量为m、电阻不计的金属杆ab。
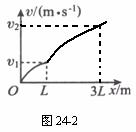
(1)若ab杆在平行于斜面的恒力作用下由静止开始沿斜面向上运动,其速度一位移关系图像如图24-2所示,则在经过位移为3L的过程中电阻R上产生的电热Q1是多少?
(2)ab杆在离开磁场前瞬间的加速度是多少?
 (3)若磁感应强度B=B0+kt(k为大于0的常数),要使金属杆ab始终静止在导轨上的初始位置,试分析求出施加ab杆的平行于斜面的外力。
(3)若磁感应强度B=B0+kt(k为大于0的常数),要使金属杆ab始终静止在导轨上的初始位置,试分析求出施加ab杆的平行于斜面的外力。
黄浦区2009学年度第一学期期终基础学业测评
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com